1、简答题  如图所示，固定在水平地面上的桌子，高度h=0.8m，桌面上放着一块木板，木板的质量M=1.0kg，长度L=1.5m，厚度可以忽略不计，木板左右两端与桌面的两端对齐．质量m=1.0kg的小物块放在距木板左端d=0.5m处（小物块可视为质点）．木板与桌面间的摩擦忽略不计．现对木板施加一个F=12N水平向右的恒力，木板与物块发生相对滑动，经过一段时间物块离开木板，在桌面上运动一段距离后，从桌面的右端滑出，最后落在地面上．取g=10m/s2．求：
（1）物块在木板上运动的时间；
（2）物块落地点与桌面右端的水平距离．

参考答案：如图分别对M和m进行受力分析和运动分析有：

（1）小物块在木板上滑动时，根据牛顿第二定律
f1=μ1mg=ma1
a1=μ1g=4.0m/s2，方向向右
木板在水平方向上的受力情况如答图1所示，根据牛顿第二定律
F-μ1mg=Ma2
a2=F-μ1mgM=8.0m/s2
设经过时间t1，物块与木板分离，
物块的位移x1=12a1t12
木板的位移x2=12a2t12
由答图2可知x2-x1=d
解得t1=0.5s
（2）物块与木板分离时，物块的速度
υ1=a1t1=2.0m/s
物块在桌面上做匀减速直线运动，设物块运动到
桌面右端时的速度为υ2，根据牛顿第二定律
f2=μ2mg=ma3
a3=μ2g=3.0m/s2，方向向左
v22-v12=2(-a3)(L-d-x1)
x1=0.5m
解得υ2=1m/s
物块做平抛运动，设经过时间t2落地
h=12gt22?t2=

本题解析：

本题难度：简单

2、选择题  如图甲所示，静止在水平地面上的物块A，受到水平拉力F的作用，F与时间t的关系如图乙所示，设物块与地面之间的最大静摩擦力fm大小与滑动摩擦力大小相等，则下列说法中错误的是

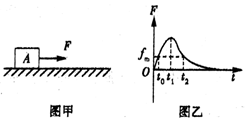
A．t0时间内加速度最小
B．t0时间内F做的功为零
C．t1时刻物块的速度最大
D．t2时刻物块的速度最大

参考答案：C

本题解析：由图可知因为拉力小于最大静摩擦力，所以0—t0这段时间内物体保持静止状态，t2--t0这段时间物体做加速运动，t2以后做减速运动，依此判断t0时刻加速度最小为零A对
0—t0这段时间内物体保持静止状态F做的功为零，B对
t2时刻物块的速度达到最大值，其后减速，C错，D对
选C

本题难度：简单

3、选择题  如图所示，将一个光滑、绝缘的挡板ABCD固定在光滑、绝缘的水平面上，AB段为直线形挡板， BCD段是半径为R的圆弧形挡板，且AB与BCD相切。挡板处于场强为E的匀强电场中，电场方向与圆直径MN平行。现将带电量为q、质量为m的小球从挡板内侧的A点由静止释放，小球沿挡板内侧恰好过M点运动到D点后抛出，下列判断正确的是?

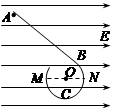
A．小球带正电或带负电均可完成上述运动过程
B．小球运动到N点时动能最大
C．AN两点间沿电场线方向的距离为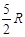
D．小球运动到C点时，挡板对小球的弹力为3qE

参考答案：BCD

本题解析：根据小球的受力情况可知，小球只能带正电才可完成上述运动过程；小球运动到N点时，电场力做功最多，所以动能最大；因为小球沿挡板内侧恰好过M点，则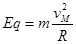,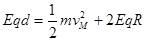，解得d=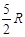;小球运动到C点时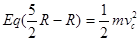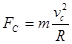，?，解得Fc=3qE.。选项BCD正确。

本题难度：一般

4、选择题  对牛顿第二定律的理解，正确的是（　　）
A．如果一个物体同时受到两个力的作用，则这两个力各自产生的加速度互不影响
B．如果一个物体同时受到几个力的作用，则这个物体的加速度等于所受各力单独作用在物体上时产生加速度的矢量和
C．平抛运动中竖直方向的重力不影响水平方向的匀速运动
D．物体的质量与物体所受的合力成正比，与物体的加速度成反比

参考答案：A、合运动与分运动具有独立性，所以两个力各自产生的加速度互不影响，A正确；
B、加速度是矢量，其合加速度满足矢量合成的法则平行四边形定则，即物体的加速度等于所受各力单独作用在物体上时产生加速度的矢量和，B正确；
C、由分运动的独立性，平抛运动中竖直方向的重力不影响水平方向的匀速运动，C正确；
D、牛顿第二定律a=Fm，加速度与合外力成正比与物体的质量成反比，而质量是物质本身的固有属性，不随运动状态改变而改变，D错误．
故选：ABC．

本题解析：

本题难度：简单

5、简答题  某兴趣小组设计了一种实验装置，用来研究碰撞问题，其模型如图所示不用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔，从左到右，球的编号依次为1、2、3…N，球的质量依次递减，每球质量与其相邻左球质量之比为k（k＜1）．将1号球向左拉起，然后由静止释放，使其与2号球碰撞，2号球再与3号球碰撞…所有碰撞皆为无机械能损失的正碰．（不计空气阻力，忽略绳的伸长，g取10m/s2）
（1）设与n+1号球碰撞前，n号球的速度为vn，求n+1号球碰撞后的速度．
（2）若N=5，在1号球向左拉高h的情况下，要使5号球碰撞后升高16k（16h小于绳长）问k值为多少？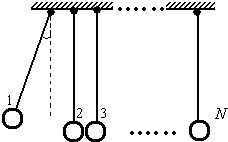

参考答案：（1）本题中的两球相碰，均可看成是“一静一动弹性碰撞模型”．因为每个球的质量依次递减，碰后不会出现入射球反弹的情况．如果入射球质量为m1，被碰球质量为m2，碰前m1的速度为v1，碰后两球的速度分别为v1′、v2′由动量守恒定律和机械能守恒定律得：
m?v1=m1v1′+m2v2′
12mV12=12mV′12+12mV′22
得：V′1=m1-m2m1+m2V1?V′2=2?m1m1+m2V1?
本题主要应用v2′当n取代1时，n+1就取代2．
设n号球质量为m，与n+1号球碰撞后的速度分别为vn′、vn+1′取水平向右为正方向，据题意有n号球与n+1号球碰撞前的速度分别为vn、0、mn+1=kmn?
根据动量守恒，有mnVn=mnV′n+kmnV′n+1…①
根据机械能守恒，有12mnVn2=12mnV′n2+12kmnV′n+12…②
由①②得：V′n+1=2Vnk+1(V′n+1=0舍去)…③
（2）设1号球摆至最低点时的速度为v1，由机械能守恒定律有：
m1gh=12m1V12…④
v1=

本题解析：

本题难度：一般