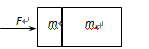
1、选择题  1966年曾在地球的上空完成了以牛顿第二定律为基础的测定质量的实验。实验时，用宇宙飞船（质量为m）去接触正在轨道上运行的火箭（质量为mx，发动机已熄火），如图所示。接触以后，开动飞船尾部的推进器，使飞船和火箭共同加速，推进器的平均推力为F，开动时间Δt，测出飞船和火箭的速度变化是Δv，下列说法正确的是?

A．火箭质量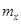应为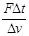
B．宇宙飞船的质量m应为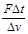
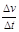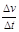C．推力F越大，就越大，且与F成正比
D．推力F通过飞船传递给火箭，所以飞船对火箭的弹力大小应为F

参考答案：C

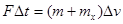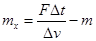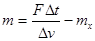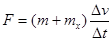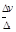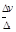本题解析：对火箭和飞船组成的整体，运用冲量定理可得，所以火箭的质量应该为，宇宙飞船的质量为，所以推力F越大，就越大，且与F成正比。对AB错误，C正确。对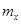分析可得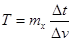，小于推力F.所以D错误。

本题难度：简单

2、填空题  A?用速度为v的质子

参考答案：质子?11H动量的增量为△P=-mv′-mv=-m（v+v′）．
根据动量守恒定律得
? mv=-mv′+4mV
得? V=v+v′4，即氦原子核?42He获得的初速度为v+v′4．
故答案为：-m?（v+v′），v+v′4．

本题解析：

本题难度：一般

3、填空题  光滑水平面上两小球a、b用不可伸长的松弛细绳相连。开始时a球静止，b球以一定速度运动直至绳被拉紧，然后两球一起运动，在此过程中两球的总动量___________（填“守恒”或“不守恒”）；机械能___________（填“守恒”或“不守恒”）。

参考答案：守恒，不守恒

本题解析：

本题难度：一般

4、简答题  （1）氢原子的部分能级如图1所示．已知可见光的光子能量在1.62eV到3.11eV之间．由此可推知，氢原子______
A．从高能级向n=1能级跃迁时发出的 光的波长比可见光的短
B．从高能级向n=2能级跃迁时发出的光均为可见光
C．从n=3能级向n=2能级跃迁时发出的光为可见光
D．从n=4能级向n=2能级跃迁时发出的光为可见光
E．从高能级向n=3能级跃迁时发出的光的频率比可见光的高
（2）在光滑水平面上静置有质量均为m的木板AB和滑块CD，木板AB上表面粗糙．动摩擦因数为μ，滑块CD上表面是光滑的1/4圆弧，其始端D点切线水平且在木板AB上表面内，它们紧靠在一起，如图所示．一可视为质点的物块P，质量也为m，从木板AB的右端以初速度v0滑上木板AB，过B点时速度为v0/2，又滑上滑块CD，最终恰好能滑到滑块CD圆弧的最高点C处，求：
①物块滑到B处时木板的速度vAB
②滑块CD圆弧的半径R．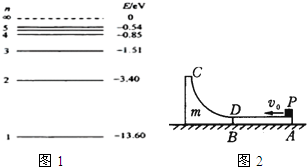

参考答案：（1）A、从高能级向n=1能级跃迁时辐射的最小光子能量为10.2eV，大于可见光的光子能量，知从高能级向n=1能级跃迁时发出的光的波长比可见光的短．故A正确．
B、从高能级向n=2能级跃迁时发出的光的光子能量可能大于3.11eV，不一定为可见光．故B错误．
C、从n=3能级向n=2能级跃迁时辐射的光子能量为1.89eV，为可见光．故C正确．
D、从n=4能级向n=2能级跃迁时发出的光子能量为2.55eV．为可见光．故D正确．
E、从高能级向n=3能级跃迁时最大的光子能量为1.51eV，小于可见光的光子能量，知从高能级向n=3能级跃迁时发出的光的频率比可见光的低．故E错误．
故答案为：A?C?D
（2）①由点A到点B时，取向左为正．由动量守恒得mv0=mvB+2m?vAB
则vAB=v04
②由点D到点C，滑块CD与物块P的动量守恒，机械能守恒，得：m?v02+m?v04=2mv共
mgR=12m(v02)2+12m(v04)2-12×2mv共2
解之得：v共=38v0，R=v0264g．
答：①物块滑到B处时木板的速度vAB=v04．
②滑块CD圆弧的半径R=v0264g．

本题解析：

本题难度：一般

5、计算题  如图所示，光滑水平面MN的左端M处有一弹射装置P，右端N处与水平传送带理想连接。传送带水平部分长L＝8m，并以恒定速度v＝3m/s沿图示箭头方向移动。质量均为m＝1kg、静止于MN上的物块A、B（视为质点）之间压缩一轻弹簧，贮有弹性势能EP＝16J。若A、B与传送带间的动摩擦因数μ＝0.2，则解除弹簧压缩，弹开物块A、B后，求：
（1）物块B在传送带上向右滑行的最远距离L1；
（2）物块B返回到水平面MN时的速度vB′；
（3）若物块B返回水平面MN后，与被弹射装置P弹回的物块A在水平面MN上弹性碰撞（碰撞过程无动能损失，碰撞时间极短），使物块B从传送带水平部分的右端Q滑出，则弹射装置P必须给物块A至少做多少功？

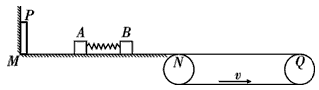
参考答案：解：（1）解除锁定后弹簧恢复原长时，A、B的速度大小分别为vA、vB，
由系统机械能守恒、动量守恒mBvB＝mAvA?

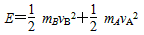
联立解得vA＝vB＝4m/s
设B沿传送带向右滑行的最远距离为L1，由功能关系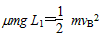
解得L1＝4m
（2）因为v＝4m/s＞3m/s，所以B返回时先加速再随传送带一起运动，
B返回到水平面MN时的速度vB′＝3m/s
（3）以A为研究对象，设碰后A、B的速度分别为vA′、vB′′，
由动能定理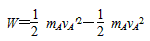
B能从Q端滑出一定有?
A与B质量相等，完全弹性碰撞后速度互换，则A的速度vA′＝vB′′
联立解得 W≥8J。

本题解析：

本题难度：困难