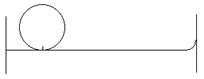
1、填空题  如图所示，虚线框内空间中同时存在着匀强电场和匀强磁场，匀强电场的电场线竖直向上，电场强度E=6×104伏/米，匀强磁场的磁感线未在图中画出．一带正电的粒子按图示方向垂直进入虚线框空间中，速度v=2×105米/秒．如要求带电粒子在虚线框空间做匀速直线运动，磁场中磁感线的方向是?，磁感应强度大小为?特。(粒子所受重力忽略不计)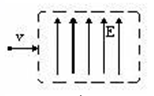

参考答案：垂直低面向外，0．3特

本题解析：带电粒子在复合场中做匀速直线运动，受到竖直向上的电场力和竖直向下的洛伦兹力，由左手定则可知磁场方向垂直纸面向外，由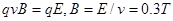
点评：难度较小，粒子在复合场中能够做匀速直线运动的条件是受力平衡，当电场力等于洛伦兹力时沿直线运动

本题难度：简单

2、计算题  如图所示，以正方形abcd为边界的区域内有平行x轴指向+x方向的匀强电场和垂直纸面向星的匀强磁场，正方形的边长为L，带电粒子（不计重力）从Oc边的中点D，以某一初速度沿y轴正方向射入场区，恰好做直线运动。如果撤去磁场，保留电场，粒子仍以上述初速度从D点射入场区，则粒子从bc边的P点射出场区，设P点的坐标为（L，yp）。求：如果撤去电场，保留磁场，粒子仍以 上述的初速度从D点射入场区，在yP取不同值的情况下，粒子出射点在场区边界上的分布范围。

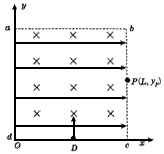
参考答案：解：设电场强度为E，磁感应强度为B，粒子电量为q，质量为m，初速度为v
当电场和磁场同时存在时，有：qBv=qE ①
撤去磁场，粒子在电场中的偏转距离为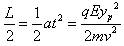 ②
撤去电场，设粒子在磁场中做圆周运动的半径为R。由洛伦兹力提供向心力，有 ③
在磁场中的偏转距离为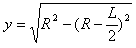 ④
由①②③④可得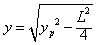： ⑤
由⑤可知，当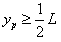时，y≥0，即粒子从纵轴上射出 ⑥
当yp=L时，由⑤得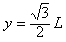： ⑦
所以，当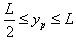时，x=0，粒子出射点在纵轴上分布范围是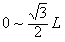： ⑧
当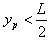时，纵坐标y=0，出射点在横坐标上的分布范围是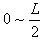： ⑨

本题解析：

本题难度：困难

3、计算题  如图所示，匀强磁场磁感应强度 B＝0.2T，磁场宽度 L＝0.3m， 一正方形金属框边长 ab＝0.1m， 每边电阻R＝0.2W，金属框在拉力F作用下以v＝10m/s的速度匀速穿过磁场区，其平面始终保持与磁感线方向垂直．求：

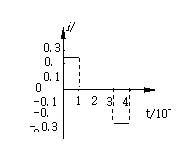
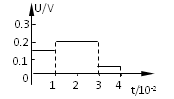
小题1:画出金属框穿过磁场区的过程中，金属框内感应电流i和a、b两端电压Uab随时间t的变化图线（规定以adcba为正方向）；
小题2:金属框穿过磁场区域的过程中，拉力F做的功；
小题3:金属框穿过磁场区域的过程中，导线ab上所产生的热量．

参考答案：
小题1:

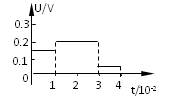
小题2:1×10-3J
小题3:Qab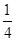＝W＝2.5×10-4J

本题解析：小题1:当ab边或cd边只有一条边处于磁场中时，电路中电流为，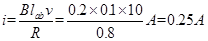
当均处于磁场中时，没有感应电流。
如图所示

第1秒，只有ab边产生感应电动势，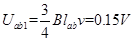
第2、3秒，回路中没有感应电流但有感应电动势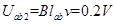
第4秒，只有cd边产生感应电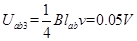动势，感应电动势
如图所示

小题2:第1 秒和第4秒所受安培力为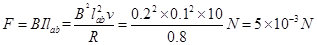
线框匀速运动，所以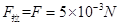
则拉力做的功为，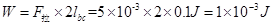
小题3:线框匀速运动，拉力做功，四条边产生热量，所以ab边产生的热量为，Qab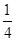＝W＝2.5×10-4J

本题难度：一般

4、计算题  （22分）如图所示，在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场，在第四象限内有一垂直于平面向里的匀强磁场，现有一质量为m、电量为+q的粒子（重力不计）从坐标原点O射入磁场，其入射方向与y的方向成45°角。当粒子运动到电场中坐标为（3L，L）的P点处时速度大小为v0,方向与x轴正方向相同。求：

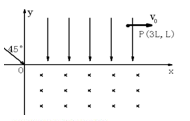
（1）粒子从O点射入磁场时的速度v；
（2）匀强电场的场强E0和匀强磁场的磁感应强度B0；
（3）粒子从O点运动到P点所用的时间.

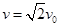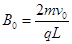参考答案：（1）（2）（3）

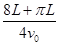
本题解析：（1）粒子从O点进入匀强磁场后在洛伦兹力作用下做匀速圆周运动，则其运动轨迹如图所示，经过磁场后进入电场，到达P点?（2分）

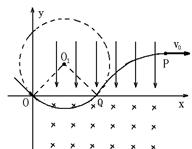
假设粒子在O点时的速度大小为v，OQ段为圆周，QP段为抛物线。
根据洛伦兹力与速度垂直不做功 可知粒子在Q点时的速度大小也为v，根据对称性可知方向与x轴正方向成45°角，可得：
Q点速度大小为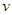，方向与X轴成斜向上。
进入电场后，电场力为竖直方向，水平方向匀速直线运动，所以有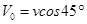? (2分)
解得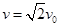：? (1分)
（2）在粒子从Q运动到P的过程中，由动能定理得：
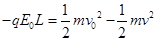? (2分)
解得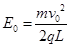：?（1分）
又在匀强电场由Q到P的过程中，
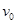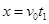水平方向匀速直线运动的速度，为位移为?（1分）
竖直方向初速度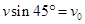匀减速到0的位移为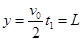?（1分）
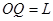可得，?（2分）
由几何关系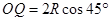可得粒子在OQ段圆周运动的半径：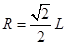
根据洛伦兹力提供向心力得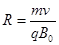
得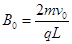?（2分）
（3）在Q点时，竖直分速度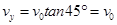? (1分)
设粒子从Q到P所用时间为,在竖直方向上有：t1=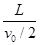=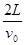? (1分)
粒子从O点运动到Q运动的圆心角为90度，所用的时间为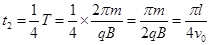： ?(1分)
则粒子从O点运动到P点所用的时间为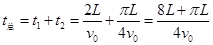：?(1分)

本题难度：一般

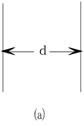
5、计算题  （20分）如图（a）所示，两块足够大的平行金属板竖直放置，板间加有匀强电场和磁场，电场和磁场的大小随时间按图（b）和图（c）所示的规律变化（规定垂直于纸面向外为磁感应强度的正方向）。在t=0时，由负极板内侧释放一初速度为零的带负电粒子，粒子的重力不计。在t=37t0/12时，带电粒子被正极板吸收。已知电场强度E0、粒子的比荷q/m以及t0。而磁感应强度B1、B2(均未知)的比值为1﹕3，在t0～2t0时间内，粒子在磁场中做匀速圆周运动的周期为t0。求：
（1）当带电粒子离负极板的距离S0="q" E0t02/2m时，粒子在两极板间运动的时间；
（2）两平行板间的距离d 。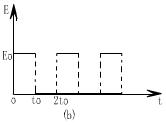

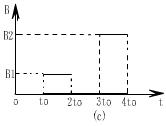
参考答案：(1) 对应的时刻为:t0、3t0/2、2t0（2）d = 2E0qt02/m + E0qt02/3лm

本题解析：解:(1)由牛顿第二定律及运动学公式:

E0q =" ma?" …… (2分)
S1 = at02/2 …… (2分)
S1 = E0qt02/2m
∵ S1 = S0
∴如图：当 S1 = S0 = E0qt02/2m时,
对应的时刻为:t0、3t0/2、2t0 .(3分)
（2）由粒子的运动情况,前3t0时间内,粒子匀加速的时间为2t0,做圆周运动时间为t0,则粒子匀加速直线运动的位移
S = a(2t0)2/2 = 4S0?…… (2分)
最后t0/12粒子做圆周运动,设粒子的速度为v2,
V2 = 2at0?…… (1分)
设粒子在磁场B2中的轨道半径为R2,
B2v2q = mv22/R2?…… (2分)
粒子在B1磁场中运动的周期T1 = 2лm/qB1 = t0…… (2分)
解得：R2 = E0qt02/3лm …… （1分）
∵粒子在B2中的周期：T2 = 2лm/qB2 = t0/3 …… (2分)
∴t0/12时间内粒子转过的角度θ=л/2 …… (1分)
即:d = S+R2…… (1分)
解得：d = 2E0qt02/m + E0qt02/3лm?……?（1分）

本题难度：一般