1、填空题 2008年8月在我国北京举行的奥运会蹦床比赛中,我国男、女运动员均获得金牌。假设表演时运动员仅在竖直方向运动,通过传感器将弹簧床面与运动员间的弹力随时间的变化规律在计算机上绘制出如图所示的曲线,当地重力加速度取10 m/s2。依据图像给出的信息可知,运动过程中运动员的质量为____,运动过程中运动员的最大加速度值为____。
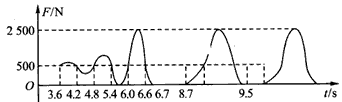
参考答案:50 kg,40 m/s2
本题解析:
本题难度:一般
2、选择题 如图为蹦极运动的示意图。弹性绳的一端固定在O点,另一端和运动员相连。运动员从O点自由下落,至B点弹性绳自然伸直,经过合力为零的C点到达最低点D,然后弹起。整个过程中忽略空气阻力。分析这一过程,下列表述正确的是

[? ]
A.经过B点时,运动员的速率最大
B.经过C点时,运动员的速率最大
C.从C点到D点,运动员的加速度增大
D.从C点到D点,运动员的加速度不变
参考答案:BC
本题解析:
本题难度:一般
3、选择题 如图所示,在光滑地面上,水平外力F拉动小车和木块一起做无相对滑动的加速运动。小车质量是M,木块质量是m,力大小是F,加速度大小是a,木块和小车之间动摩擦因数是μ。则在这个过程中,木块受到的摩擦力大小是

[? ]
A.μmg
B.
C.μ(M+m)g
D.ma
参考答案:BD
本题解析:
本题难度:一般
4、计算题 “翻滚过山车”的物理原理可以用如图 所示装置演示,光滑斜槽轨道AD与半径为R=0.1m的竖直圆轨道(圆心为O)相连,AD与圆O相切于D点,B为轨道的最低点,∠DOB=37°.质量为m=0.1kg的小球从距D点L=1.3m处由静止开始下滑,然后冲上光滑的圆形轨道(g=10m/s2,sin37°=0.6,cos37°=0.8).求:
所示装置演示,光滑斜槽轨道AD与半径为R=0.1m的竖直圆轨道(圆心为O)相连,AD与圆O相切于D点,B为轨道的最低点,∠DOB=37°.质量为m=0.1kg的小球从距D点L=1.3m处由静止开始下滑,然后冲上光滑的圆形轨道(g=10m/s2,sin37°=0.6,cos37°=0.8).求:
(1)小球在光滑斜槽轨道上运动的加速度的大小;
(2)小球通过B点时对轨道的压力的大小;
(3)试分析小球能否通过竖直圆轨道的最高点C,并说明理由.
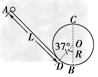
参考答案:解:(1)在光滑斜槽上由牛顿第二定律得:
mgsin37°=ma.
故a=gsin37°=6m/s2
(2)小球由A至B,机械能守恒,
则mg(Lsin37°+hDB)=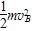
hDB=R(1-cos37°)
又小球在B点,由牛顿第二定律得:
FNB=mg+ =17N
=17N
由牛顿第三 定律得:小球过B点时对轨道的压力大小为17N.
定律得:小球过B点时对轨道的压力大小为17N.
(3)小球要过最高点,需要的最小速度为v0
则mg= 即v0=
即v0= =1m/s
=1m/s
又小球从来源:91exam .orgA到C机械能守恒,
所以mg[Lsin37°-R(1+cos37°)]= mv
mv
解之vC= m/s>1m/s
m/s>1m/s
故小球能过最高点C.
本题解析:
本题难度:一般
5、计算题 质量为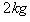 的物体在水平推力
的物体在水平推力 的作用下沿水平面作直线运动,一段时间后撤去
的作用下沿水平面作直线运动,一段时间后撤去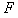 ,其运动的
,其运动的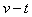 图像如图所示。
图像如图所示。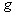 取
取 ,求:
,求:
(1)物体与水平面间的运动摩擦因数 ;
;
(2)水平推力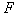 的大小;
的大小;
(3)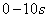 内物体运动位移的大小。
内物体运动位移的大小。

参考答案:解:以物体的运动方向为正方向。在 内,对物体受力分析如图所示: ?
内,对物体受力分析如图所示: ? 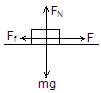 由牛顿第二定律得
由牛顿第二定律得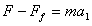 ①
①
由速度图象可知 ②
②
在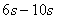 内,对物体受力分析如图所示:?
内,对物体受力分析如图所示:? 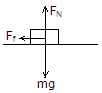 由牛顿第二定律得
由牛顿第二定律得 ③
③
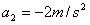 ?④
?④
又有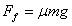 ⑤
⑤
联立①②③④⑤式解得 ,
,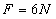
在速度图象中,由位移和对应“面积”的关系可知,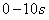 内物体运动位移的大小
内物体运动位移的大小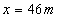
本题解析:
本题难度:困难