1、简答题  甲、乙两物体相距s，在同一直线上同方向做匀减速运动，速度减为零后就保持静止不动．甲物体在前，初速度为v1，加速度大小为a1．乙物体在后，初速度为v2，加速度大小为a2且知v1＜v2，但两物体一直没有相遇，求甲、乙两物体在运动过程中相距的最小距离为多少？

参考答案：若是v1a1≤v2a2，说明甲物体先停止运动或甲乙同时停止运动．
在运动的过程中，乙的速度一直大于甲的速度，只有两物体都停止运动时，才相距最近．
可知最近距离△s=s+v122a1-v222a2．
若是v1a1＞v2a2，说明乙物体先停止运动，那么两物体在运动过程中总存在速度相等的时刻，此时两物体相距最近．
根据v共=v1-a1t=v2-a2t
解得t=v2-v1a2-a1．
在t时间内，甲的位移s1=v共+v12t，乙的位移s2=v共+v22t
代入表达式△s=s+s1-s2
解得△s=s-v2-v12(a2-a1)．
答：甲、乙两物体在运动过程中相距的最小距离为△s=s+v122a1-v222a2或△s=s-v2-v12(a2-a1)．

本题解析：

本题难度：一般

2、选择题  一辆汽车以20m/s的速度作匀速直线运动，从某时刻开始汽车紧急刹车，刹车后的加速度大小为4.0m/s2，则从刹车起，汽车在6.0秒末的速度大小是
A.0m/s
B.2.0m/s
C.2.4m/s
D.4.0m/s

参考答案：A

本题解析：分析：根据匀变速直线运动速度时间公式求出汽车刹车到停止所需的时间，判断汽车是否停止，因为汽车速度为零后不再运动．
解答：根据匀变速直线运动的时间公式得，汽车刹车到停止所需的时间t0==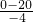s=5s＜6s．知6s末速度为零．故A正确，B、C、D错误．
故选A．
点评：解决本题的关键掌握匀变速直线运动运动学公式，并能灵活运用．注意该问题属于“刹车”问题．

本题难度：一般

3、计算题  如图所示，小菲在超市里推车购物，若小车和货物的总质量为10kg，小车在水平推力的作用下由静止开始沿水平地面做匀加速直线运动，加速度大小为0.5m/s2，小车运动了4s，小车运动中所受的阻力恒为2N，求：

（1）推力的大小；
（2）4s末小车的速度大小；
（3）4s后撤销推力，小车还能向前运动多远。

参考答案：（1）7N（2）2m/s（3）10m

本题解析：（1）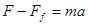
?
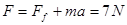（2）?
（3）
?
点评：此类题型结合牛顿运动定律分析出物体加速度，结合物体的运动规律，利用匀变速直线运动规律公式简单计算即可。

本题难度：一般

4、简答题  一辆汽车正以30m/s的速度在平直路面上行驶，驾驶员突然发现正前方约60m处有一个障碍物，驾驶员经0.2s反应时间后立即以8m/s2的加速度刹车．试判断汽车经过2s后是否会撞上障碍物？（要求列出算式，写出求解过程）

参考答案：在驾驶员的反应时间内汽车仍做匀速直线运动，则在司机的反应时间内汽车通过的位移为
? x1=vt1=30×0.2m=6m．
刹车2s后汽车通过的位移为? x2=vt2+12at22=30×2-12×8×22=44（m），
则总位移为 x=x1+x2=50m＜60m
故汽车不会撞上障碍物．
答：汽车经过2s后不会撞障碍物．

本题解析：

本题难度：一般

5、选择题  如图所示为甲、乙两个质点的速度—时间图象，根据图象可知（?）

A．甲做匀变速直线运动，乙做匀速直线运动
B．甲、乙两质点在t=0时刻的位置不一样
C．甲、乙两质点在t="2" s时刻相遇
D．在前4 s内甲、乙两质点的位移相等

参考答案：D

本题解析：物体在第1 s末速度开始减小，方向不变，A错.由图象知，物体第2 s内的速度方向和第3 s内的速度方向是相反的，B错.物体在前2 s内都向前运动，故2 s末不会返回到出发点，C错.物体在2 s至4 s内，处于返回阶段，通过计算（或根据面积等于位移）可知，物体在第4 s末返回到出发点，D对.

本题难度：简单