1、选择题  关于电荷在磁场中运动速度、磁场和电荷受到洛仑兹力三者之间的方向关系如图所示，其中正确的是（?）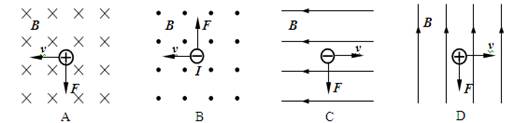

参考答案：A

本题解析：考点：
分析：左手定则的内容：伸开左手，使四指与大拇指垂直，且在同一个平面内，让磁感线穿过掌心，四指方向与正电荷的运动方向相同，大拇指所指的方向为洛伦兹力的方向．
解答：解：根据左手定则得，A选项洛伦兹力方向竖直向下，B选项洛伦兹力方向竖直向下，C选项不受洛伦兹力，D选项洛伦兹力方向垂直纸面向外．故A正确，B、C、D错误．
故选A．
点评：解决本题的关键掌握左手定则判定电荷在磁场中运动速度、磁场和电荷受到洛仑兹力三者之间的方向关系．

本题难度：简单

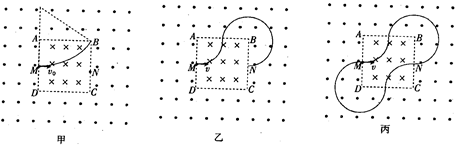
2、计算题  一块N型半导体薄片（称霍尔元件），其横载面为矩形，体积为b×c×d，如图所示。已知其单位体积内的电子数为n、电阻率为ρ、电子电荷量e，将此元件放在匀强磁场中，磁场方向沿z轴方向，并通有沿x轴方向的电流I。

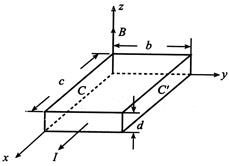
(1)此元件的CC/两个侧面中，哪个面电势高？
(2)试证明在磁感应强度一定时，此元件的CC/ 两个侧面的电势差与其中的电流成正比；
(3)磁强计是利用霍尔效应来测量磁感应强度B的仪器。其测量方法为：将导体放在匀强磁场之中，用毫安表测量通以电流I，用毫伏表测量C、C/间的电压U， 就可测得B。若已知其霍尔系数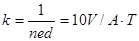，并测得U =0.6mV，I=3mA。试求该元件所在处的磁感应强度B的大小。

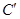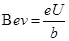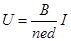参考答案：⑴电势较高，（2）由I=nebdv和得，所以侧面的电势差与其中的电流成正比，（3）0.02T

本题解析：⑴电子在洛伦兹力作用下向侧面C移动，故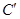电势较高 ?
（2）假设定向移动速度为v，
由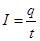，q="nebdvt" 可得 I=nebdv?
稳定时有：?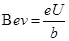
可得·?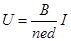
由于B、n、e、d均为定值 ，所以侧面的电势差与其中的电流成正比?
（3）由上可知?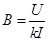
代入数据可得：B=0.02T?
点评：本题中左手定则判定电子的偏转方向，找到电势高的面，随着电荷的积累，两面间电压增大，最终稳定后电子在洛伦兹力和电场力的作用下处于平衡，根据平衡，结合电流的微观表达式，可得出两个侧面的电势差与其中的电流的关系．

本题难度：一般

3、计算题  （18分）如图所示，竖直平面内边长为a的正方形ABCD是磁场的分界线，在正方形的四周及正方形区域内存在方向相反、磁感应强度的大小均为B的与竖直平面垂直的匀强磁场，M、N分别是边AD、BC的中点。现有一质量为m、电荷量为q的带正电粒子从M点沿MN方向射出，带电粒子的重力不计。

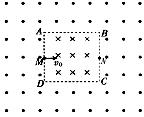
（1）若在正方形区域内加一与磁场方向垂直的匀强电场，恰能使以初速度v0射出的带电粒子沿MN直线运动到N点，求所加电场的电场强度的大小和方向。
（2）为使带电粒子从M点射出后，在正方形区域内运动到达B点，则初速度v0应满足什么条件?
（3）试求带电粒子从M点到达N点所用时间的最小值，并求出此条件下粒子第一次回到M点的时间。

参考答案：（1）E=Bv0方向竖直向下 ?（2）v0=5aqB/4m?（3）t’=2T=4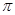m/qB

本题解析：（1）由题意，电场力与洛伦兹力平衡，有：qE=qv0B
解得E=Bv0
因带电粒子带正电，知电场强度的方向竖直向下
（2）此时，带电粒子的运动轨迹如图甲所示，
根据几何关系得R2=a2+(R-a/2)2
解得R=5a/4
由牛顿第二定律得qv0B=mv02/R
解得v0=5aqB/4m
（3）由题意可画出带电粒子的运动轨迹如图乙所示，可得带电粒子在两磁场中的轨道半径均为r=a/2
带电粒子在正方形区域内的运动时间t1=T/4
在正方形区域外的运动时间t2=3T/4
由qvB=4 m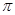2r/T2，可得T=2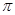m/qB
故带电粒子从M点到达N点所用时间的最小值t=t1+t2=2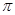m/qB ,
画出带电粒子从N点继续运动的轨迹如图丙所示，知带电粒子可以回到M点，由对称性，回到M点的时间为t’=2T=4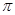m/qB

本题难度：一般

4、选择题  如图所示，在两个不同的匀强磁场中，磁感应强度关系为B1=2B2，当不计重力的带电粒子从B1垂直磁场运动到B2，则粒子的（?）

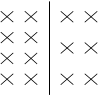
B1?B2
A．速率将加倍
B．轨道半径将加倍
C．周期将加倍
D．做圆周运动的角速度将加倍

参考答案：BC

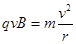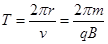本题解析：因洛伦兹力不做功，得粒子运动的速率不变，A错；由得到知轨道半径将加倍，B对；由知周期将加倍，C对；由知做圆周运动的角速度将减小为原来的一半，D错。
点评：学生明确洛伦兹力永不做功，能熟练运用半径公式，周期公式，角速度与周期的关系式解相关问题。

本题难度：简单

5、选择题  一束几种不同的正离子, 垂直射入正交的匀强磁场和匀强电场区域里, 离子束保持原运动方向未发生偏转. 接着进入另一匀强磁场, 发现这些离子分成几束如图. 对这些离子, 可得出结论:

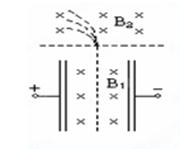
A．它们的动能一定各不相同
B．它们的电量一定各不相同
C．它们的质量一定各不相同
D．它们的比荷一定各不相同

参考答案：D

本题解析：粒子在磁场和电场正交区域里，同时受到洛伦兹力和电场力作用，粒子没有发生偏转，说明粒子所受电场力和洛伦兹力平衡，满足qvB=qE，即不发生偏转的粒子具有共同的速度大小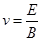，粒子进入磁场后受洛伦兹力作用做匀速圆周运动，满足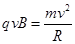，圆周运动的半径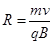，由此进行分析得出结论．
解：经过速度选择器后的粒子速度相同，粒子所受电场力和洛伦兹力平衡，满足qvB=qE，即不发生偏转的粒子具有共同的速度大小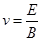；进入磁场区分开，轨道半径不等，根据公式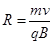，只能说明比荷不同，故A错误，B错误，C错误，D正确；
故选:D

本题难度：一般