1、计算题  现检测汽车A的制动性能：以标准速度20m/s在平直公路上行驶时，制动后40s停下来，若A在平直公路上 以20m/s的速度行驶时发现前方180m处有一货车B以6m/s的速度同向匀速行驶，司机立即制动，能否发 生撞车事故？

参考答案：

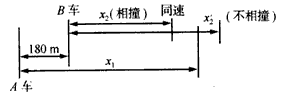
解：如图，汽车A以v0=20m/s的初速度做匀减速直线运动经40s停下来。据加速度公式可求出a=0.5m/s2。当A车减为与B车同速时，是A车逼近B车距离最多的时刻，这时若能超过B车则相撞，反之则不能相撞
?
据v2-v02=2ax可求出A车减为与B车同速时的位移x1=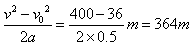
此时间t内B车的位移为x2，则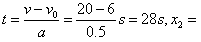v2t=6×28m=168m
△x=364m-168m=196m>180m，所以两车相撞

本题解析：

本题难度：一般

2、简答题  赛车从静止启动作匀加速直线运动，加速度为a1，一段时间后立即改作匀减速直线运动，加速度的大小为a2（a2表示正数），直至速度变为0，全过程的总时间为t，求：
（1）加速过程与减速过程的时间之比
（2）加速过程与减速过程的位移之比
（3）全过程的总位移大小．

参考答案：（1）赛车从静止启动作匀加速直线运动，后改作匀减速直线运动，两段过程的速度改变量相等，即：
vm=a1t1=a2t2
得：t1：t2=a2：a1
（2）赛车从静止开始加速，x1=vm2t1，赛车减速的过程：x2=vm2t2，
得：x1：x2=t1：t2=a2：a1
（3）赛车的总位移：x=vm2t1+vm2t2=vm2t
t=t1+t2=vma1+vma2=vm(a1+a2)a1a2
联立以上两式，得：x=a1a2t22(a1+a2)
答：（1）加速过程与减速过程的时间之比t1：t2=a2：a1
（2）加速过程与减速过程的位移之比x1：x2=a2：a1
（3）全过程的总位移大小a1a2t22(a1+a2)．

本题解析：

本题难度：一般

3、计算题  如图所示，楔形物块固定在水平地面上，其斜面的倾角θ=37°。一个质量m=0.50kg的小物块以v0=8.0m/s的初速度，沿斜面向上滑行一段距离速度减为零。已知小物块与斜面间的动摩擦因数μ=0.25，sin37°=0.60，cos37°=0.80，g取10m/s2。求：

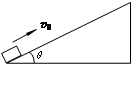
（1）小物块向上滑行过程中的加速度大小；
（2）小物块向上滑行的时间；
（3）小物块向上滑行过程中克服摩擦力所做的功。

参考答案：（1）8.0m/s2（2）1.0s（3）4.0J

本题解析：（1）小物块沿斜面向上滑行的过程中，受重力、支持力、摩擦力，
根据牛顿第二定律有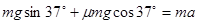
解得：a=8.0m/s2
（2）设小物块向上滑行时间为t，根据运动学公式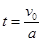
解得 ：t=1.0s
（3）小物块沿斜面向上滑行的位移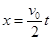
此过程中，小物块克服摩擦力做的功Wf=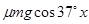
解得：Wf=4.0J
考点：牛顿第二定律的综合应用.

本题难度：一般

4、选择题  汽车自O点出发从静止开始在平直公路上作匀加速直线运动,途中在6s时间内分别经过P、Q两根电杆已知P,Q相距60m,车经过Q时的速率是15m/s,则下列说法不正确的是  （     ）
A．车的加速度为1.5m/s2
B．经过P时的速率为5m/s
C．P、O两点间距为7.5m
D．车从出发到Q所用的时间为9s