1、选择题  中俄联合火星探测器，2009年10月出发，经过3.5亿公里的漫长飞行，在2010年8月29日抵达了火星．双方确定对火星及其卫星“火卫一”进行探测．火卫一在火星赤道正上方运行，与火星中心的距离为9450km，绕火星1周需7h39min．若其运行轨道可看作圆形轨道，万有引力常量为G=6.67×10-11Nm2/kg2，则由以上信息能确定的物理量是（　　）
A．火卫一的质量
B．火星的质量
C．火卫一的绕行速度
D．火卫一的向心加速度

参考答案：根据万有引力提供向心力GMmr2=mr(2πT)2，知道了轨道半径和周期，可以求出中心天体（火星）的质量；根据v=r2πT，可求出火卫一的绕行速度，根据a=r(2πT)2，可求出火卫一的向心加速度．环绕天体（火卫一）的质量在分析已约去，不能求出．故B、C、D正确，A错误．
故选BCD．

本题解析：

本题难度：简单

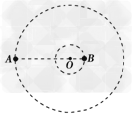
2、计算题  如图，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动，星球A和B 两者中心之间的距离为L。已知A、B的中心和O三点始终共线，A和B分别在O的两侧．引力常数为G。
(1)求两星球做圆周运动的周期；
(2)在地月系统中，若忽略其他星球的影响，可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行的周期记为T1。但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期记为T2。已知地球和月球的质量分别为5.98×1024?kg和7.35×1022?kg。求T2与T1两者平方之比．(结果保留3位小数)

参考答案：解：(1)设两个星球A和B做匀速圆周运动的轨道半径分别为r和R，相互作用的引力大小为F，运行周期为T
根据万有引力定律有F＝G?①
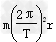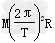由匀速圆周运动的规律得F＝ ②?F＝ ③
由题意得L＝R＋r ④
联立①②③④式得T＝2π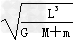 ⑤
(2)在地月系统中，由于地月系统旋转所围绕的中心O不在地心，月球做圆周运动的周期可由⑤式得出T1＝2π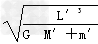 ⑥
式中，M′和m′分别是地球与月球的质量，L′是地心与月心之间的距离．若认为月球在地球的引力作用下绕地心做匀速圆周运动，则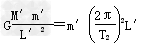?⑦
式中，T2为月球绕地心运动的周期．由⑦式得T2＝2π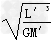 ⑧?
由⑥⑧式得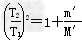
代入题给数据得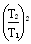＝1.012

本题解析：

本题难度：一般

3、填空题  绕太阳运行的除八大行星外，还有许多小行星和矮行星（如冥王星）等，它们的轨迹都可粗略地认为是圆，各星球半径和轨道半径的大小如下表所示：

从表中所立数据可以估算出冥王星的公转周期约为__________年。

参考答案：247

本题解析：

本题难度：一般

4、计算题  我国首个月球探测计划“嫦娥工程”将分三个阶段实施，大约用十年左右时间完成，这极大地提高了同学们对月球的关注程度．以下是某同学就有关月球的知识设计的问题，请你解答：若已知地球半径为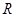，地球表面的重力加速度为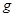，月球绕地球运动的周期为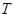，且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径。

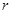参考答案：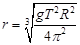

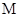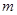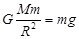本题解析：假设地球质量为，对于静止在地球表面上的物体有 ?(3分)
设月球绕地球运动的轨道半径为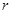，?有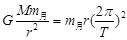? (3分)
由上面可得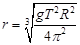：??(2分)
本题考查的万有引力的相关问题。抓住万有引力提供向心力这一特点便能轻松解除此题。

本题难度：简单

5、选择题  某同学这样来推导第一宇宙速度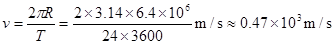，这个结果与正确值相差很远，这是由于他在处理时错误地认为
A．卫星的向心力等于它在地球表面附近所受的万有引力
B．卫星的周期等于地球自转的周期
C．卫星的轨道半径等于地球的半径
D．卫星的轨道是圆轨道

参考答案：B

本题解析：第一宇宙速度的大小等于贴近星球表面做匀速圆周运动的速度，半径等于地球的半径，但是周期与地球的周期不等。故B正确，A、C、D错误。
故选B,

本题难度：简单