1、计算题 如图所示,在场强为E=2×103 V/m的水平匀强电场中,有半径R=0.4m的光滑半圆形轨道DCB竖直放置,与水平绝缘轨道AB平滑连接,电场线与轨道平面ABCD平行,C为DB圆弧的中点。一带正电、电荷量q=5×10-5 C、质量m=20g、可视为质点的小滑块与水平轨道AB间的动摩擦因数μ=0.2,取g=10 m/s2。
(1)若小滑块从半圆形轨道上C点静止释放,运动到水平轨道上的P点静止,求小滑块通过BP段的时间是多少?
(2)若小滑块从水平轨道上的A端静止释放,沿轨道运动恰能到达并通过最高点D,求小滑块此次运动通过C点时对轨道的压力是多大?

参考答案:解:(1)设滑块过B点时的速度为vB,C到B由动能定理得: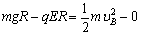
设B 到P时间为t ,由动量定理得:
解得t=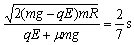
(2)设过D点的速度为v,沿轨道恰能到达最高点D的条件为:mg=mv2/R
设滑块过C点时的速度为vC,从C到D由动能定理得:
设滑块在C点时所受的压力为N,则由牛顿第二定律有: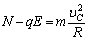
解得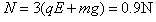
由牛顿第三定律,滑块通过C点时对轨道的压力大小N"=N=0.9N
本题解析:
本题难度:困难
2、计算题 如图,倾角为θ的斜面固定。有n个质量都为m的相同的小木块(可视为质点)放置在斜面上。相邻两小木块间距离都为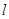 ,最下端的木块距底端也是
,最下端的木块距底端也是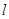 ,小木块与斜面间的动摩擦因数都为μ。在开始时刻,第一个小木块从斜面顶端以初速度v0沿斜面下滑,其余所有木块都静止,由于第一个木块的下滑将依次引起一系列的碰撞。设每次碰撞的时间极短,在每次碰撞后,发生碰撞的木块都粘在一起运动,直到最后第n个木块到达底端时,速度刚好为零。已知重力加速度为g.求:
,小木块与斜面间的动摩擦因数都为μ。在开始时刻,第一个小木块从斜面顶端以初速度v0沿斜面下滑,其余所有木块都静止,由于第一个木块的下滑将依次引起一系列的碰撞。设每次碰撞的时间极短,在每次碰撞后,发生碰撞的木块都粘在一起运动,直到最后第n个木块到达底端时,速度刚好为零。已知重力加速度为g.求:
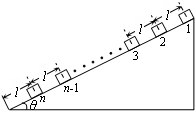
小题1:第一次碰撞后小木块1的速度大小v;
小题2:从第一个小木块开始运动到第一次碰撞后系统损失的机械能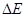 ;
;
小题3:发生一系列碰撞后,直到最后第n个木块到达底端,在整个过程中,由于碰撞所损失的总机械能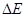 总。
总。
参考答案:
小题1: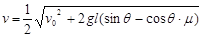
小题2:
小题3: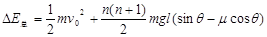
本题解析:(1)设小木块1碰前的速度为v1,从开始运动到碰前,根据动能定理
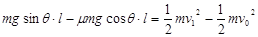 ?
?
对小木块1和2,由动量守恒?mv1 = 2mv?
求出 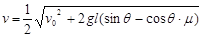 ?
?
(2)碰撞前损失的机械能为?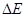 1 = μmgcosθ·l?
1 = μmgcosθ·l?
因碰撞损失的机械能为?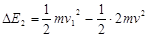 ?
?
求出  ?
?
(3)对n个木块碰撞的全过程?
重力做的总功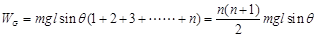
克服摩擦做的总功
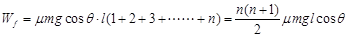 ?
?
根据功与能的关系?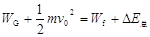 ?
?
由以上各式求出?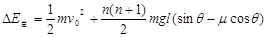
本题难度:一般
3、选择题 如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,另一个电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v.已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L则( )
A.OB间的距离为r=
B.从A到B的过程中,电场力对点电荷乙做的功W=μmgL+mv02-m
C.从A到B的过程中,电场力对点电荷乙做的功为
D.在点电荷甲形成的电场中,AB间电势差UAB=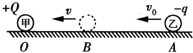
参考答案:A、当速度最小时有:mgμ=F库=kQqr2,解得:r=
本题解析:
本题难度:简单
4、简答题 如图所示,一小滑块(体积很小,可视为质点)从A点以某一水平向右的初速度出发,沿水平直线轨道运动到B点后,进入半径R=10cm的光滑竖直圆形轨道,圆形轨道间不相互重叠,即小滑块离开圆形轨道后可继续向C点运动,C点右侧有一壕沟,C、D两点的竖直高度h=0.8m,水平距离s=1.6m,水平轨道AB长为L1=2m,BC长为L2=4m,小滑块与水平轨道间的动摩擦因数μ=0.3,重力加速度g=10m/s2.
(1)若小滑块恰能通过圆形轨道的最高点,求小滑块在A点的初速度?
(2)若小滑块既能通过圆形轨道的最高点,又不掉进壕沟,求小滑块在A点的初速度的范围是多少?
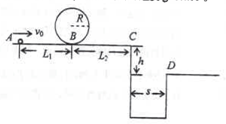
参考答案:(1)小球恰能通过最高点,重力提供向心力,有:
mg=mv2R,
由A到最高点,由动能定理的2:
μmgL1-mg?2R=12mv2-12mvA2
联立并代入数据解得在A点的初速度为:vA=
本题解析:
本题难度:一般
5、选择题 如图所示,在绝缘水平面上方存在着足够大的水平向右的匀强电场,带正电的小金属块以一定初速度从A点开始沿水平面向左做直线运动,经L长度到达B点,速度变为零.此过程中,金属块损失的动能有2/3转化为电势能.金属块继续运动到某点C(图中未标出)时的动能和A点时的动能相同,则金属块从A开始运动到C整个过程中经过的总路程为(?)
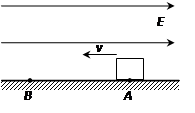
A.1.5L
B.2L
C.3L
D.4L
参考答案:D
本题解析:因有三分之二的动能转化成了电势能,故金属块损失的动能有三分之一转化为了内能,根据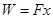 可得 可得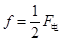 ,从A到C点全程由动能定理得 ,从A到C点全程由动能定理得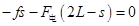 ,代入解得 ,代入解得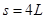 ,所以只有选项D正确; ,所以只有选项D正确;
本题难度:一般
|
|