1、计算题  （10分）跳台滑雪起源于挪威，1860年挪威德拉门地区的两位农民在奥斯陆举行的首届全国滑雪比赛上表演了跳台飞跃动作，后逐渐成为一个独立的项目并得到推广。如图为一跳台的示意图，运动员从雪道的最高点A由静止开始滑下，不借助其他器械，沿雪道滑到跳台B点后，沿与水平方向成30°角斜向左上方飞出，最后落在斜坡上C点。已知A、B两点间高度差为4m，B、C点两间高度为13m，运动员从B点飞出时速度为8ms，运动员连同滑雪装备总质量为60kg。不计空气阻力，g=10m/s2。求
（1）从最高点A滑到B点的过程中，运动员克服摩擦力做的功；
（2）运动员落到C点时的速度；
（3）离开B点后，在距C点多高时，运动员的重力势能等于动能。（以C点为零势能参考面）

参考答案：（1）…………………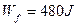
（2）……………
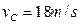（3）……………………

本题解析：解：（1）由动能能定理得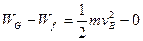：?①………………（2分）
又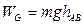?②……………………（1分）
代入数据得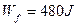：……………………（1分）
（2）从B到C由机械能守恒定律得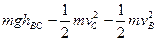：③………………（2分）
解得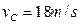：………………（1分）
（3）设离C点高h时，运动员的重力势能等于其动能，由机械能守恒定律得：
④………………（2分）
解得：……………………（1分）

本题难度：简单

2、简答题  一平行板电容器的两个极板ab、cd正对竖直放置，如图所示，极板长为L．现有一电荷量大小为q、质量为m的带电质点P自紧靠ab板内侧的某点以大小为v的初速度竖直向上射出，然后以速度v从cd板的上端c处水平进入cd板右侧的正交电场、磁场中并恰好做匀速圆周运动；当带电质点P运动到cd板上小孔O处时，有另一带电质点Q由静止释放，P、Q两带电质点在小孔处发生正碰，已知Q的质量为m/3，碰撞前Q的电性与P相同且电荷量大小为q/2，碰撞后Q运动到ab板内侧的最下端b处时仍以大小为v的速度竖直离开电容器．忽略平行板电容器两端电场的边缘效应．求：
（1）电容器两板间的电场强度大小；
（2）磁场的磁感应强度大小；
（3）带电质点P最后离开平行板电容器时的速度大小．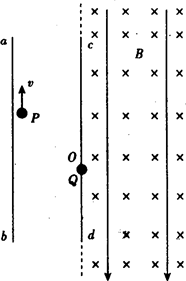

参考答案：（1）设P从出发点运动至c阶段运动的时间为t．
其中水平加速度为ax，则在水平方向上有：ax=qEm…①
v=axt=qEmt…②
在竖直方向上有：0-v=-gt…③
t=v0g…④
联立①②③得：E=mgq…⑤
（2）设电容器两极板间的距离为d．
对P从出发点至c阶段，在水平方向上有：d=v+02t…⑥
联立④⑥解得d=v22g…⑦
设在正交电场、磁场中质点P做匀速圆周运动的半径为R，则qvB=mv2R
R=mvqB…⑧
又2R+d=l…? ⑨
联立⑦⑧⑨得：B=4mgvq(2gl-v2)．
（3）设P、Q碰撞后的速度分别为v1、v2．
由动量守恒定律得，mv=mv1+m3v2
设碰撞后P、Q带电量大小分别为q1、q2，则q1+q2=32q
碰撞后Q在水平方向上有：d=v2+02t
可得：v2=v，v1=23v
0-v22=-2q2Em3d
得q1=76q，q2=q3．
则碰撞后P在水平方向上的加速度ax=q1Em=76g．
它在电容器中间运动的时间仍为t，设P射出电容器时其水平速度为vx，
则vx=v1-axt=-12v
则P射出电容器时的速度为vp，
vp=

本题解析：

本题难度：一般

3、选择题  汽车沿水平公路做匀速直线运动，下列说法正确的是
[? ]
A．汽车沿水平面运动过程中，汽车的动能与重力势能均保持不变，因而总机械能的数值不变，符合机械能守恒定律
B．汽车受到的合外力为零，因而无外力做功
C．通过每一段路程时，牵引力做功大小大于阻力做功的大小
D．因为合外力做功为零，所以动能不变

参考答案：D

本题解析：

本题难度：简单

4、简答题  如图所示，某货场利用固定于地面的、半径R=1.8m的四分之一圆轨道将质量为m1=10kg的货物（可视为质点）从高处运送至地面，已知当货物由轨道顶端无初速滑下时，到达轨道底端的速度为5m/s．为避免货物与地面发生撞击，在地面上紧靠轨道依次排放两块完全相同的木板A、B，长度均为l=2m，质量均为m2=20kg，木板上表面与轨道末端相切．货物与木板间的动摩擦因数为μ=0.4，木板与地面间的动摩擦因数μ2=0.1．（最大静摩擦力与滑动摩擦力大小相等，取g=10m/s2）
（1）求货物沿圆轨道下滑过程中克服摩擦力做的功
（2）通过计算判断货物是否会从木板B的右端滑落？若能，求货物滑离木板B右端时的速度；若不能，求货物最终停在B板上的位置．

参考答案：（1）设货物沿圆轨道下滑过程中克服摩擦力做的功为Wf，对货物，
由动能定理得：
m1gR-Wf=12m1v2
Wf=m1gR-12m1v2=55J
（2）当货物滑上木板A时，货物对木板的摩擦力f1=μ1m1g=40N
地面对木板A、B的最大静摩擦力f2=μ2（2m2+m1）g=50N
由于f1＜f2，
此时木板A、B静止不动．?
设货物滑到木板A右端时速度为v1，由动能定理：-μ1m1gl=12m1v21-12m1v2
得：v1=3m/s
当货物滑上木板B时，地面对木板A、B最大静摩擦力f3=μ2（m2+m1）g=30N
由于f1＞f3，此时木反B开始滑动．?
设货物不会从木板B的右端滑落，二者刚好相对静止时的速度为v2．
则对货物：a1=μ1g=4m/s2
v2=v1-a1t
对木板B：a2=μ1m1g-μ2(m1+m2)gm2=0.5m/s2
v2=a2t
由以上两式可得：v2=13m/s
t=23s
此过程中，s1=12(v1+v2)t=109ms2=12v2t=19m
由于s1-s2=1.0m＜l，所以货物最终未从木板B上滑了，且与其右端的距离为1.0m
答：（1）货物沿圆轨道下滑过程中克服摩擦力做的功为55J；
（2）货物最终未从木板B上滑了，且与其右端的距离为1.0m

本题解析：

本题难度：一般

5、计算题  如图所示为半径R=0.50m的四分之一圆弧轨道，底端距水平地面的高度h=0.45m。一质量m=1.0kg的小滑块从圆弧轨道顶端A由静止释放，到达轨道底端B点的速度v = 2.0m/s。忽略空气的阻力。取g =10m/s2。求：

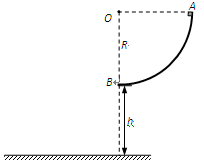
（1）小滑块在圆弧轨道底端B点受到的支持力大小FN；
（2）小滑块由A到B的过程中，克服摩擦力所做的功W；
（3）小滑块落地点与B点的水平距离x。

参考答案：（1）18N（2）3J（3）0.6m

本题解析：（1）根据牛顿第二定律，　　　?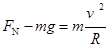
解得：?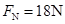
（2）根据动能定理，　　?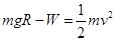
解得：?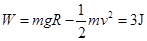
（3）水平方向：　　?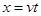
竖直方向：　 ?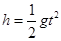
解得：?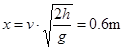
点评：小滑块由A到B的过程中，速度是变化的，滑块对圆弧的压力也是变化的，滑动摩擦力也是变化的，不能直接计算克服摩擦力所做的功，要根据动能定理来计算，还要注意列表达式时的正负号。

本题难度：一般