1、计算题  如图所示，在区域Ⅰ(0≤x≤d)和区域Ⅱ(d≤x≤2d)内分别存在匀强磁场，磁感应强度大小分别为B和2B，方向相反，且都垂直于Oxy平面．一质量为m、带电荷量q(q＞0)的粒子a于某时刻从y轴上的P点射入区域Ⅰ，其速度方向沿x轴正向．已知a在离开区域Ⅰ时，速度方向与x轴正向的夹角为30°；此时，另一质量和电荷量均与a相同的粒子b也从P点沿x轴正向射入区域Ⅰ，其速度大小是a的；不计重力和两粒子之间的相互作用力．求：

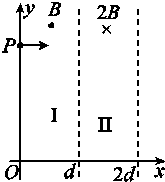
小题1:粒子a射入区域Ⅰ时速度的大小；
小题2:当a离开区域Ⅱ时，a、b两粒子的y坐标之差．

参考答案：
小题1: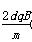
小题2:

本题解析：
(1)设粒子a在Ⅰ内做匀速圆周运动的圆心为C(在y轴上)，半径为Ra1，粒子速率为va，运动轨迹与两磁场区域边界的交点为P′，如图所示．由洛伦兹力公式和牛顿第二定律得
qvaB＝m①
由几何关系得
∠PCP′＝θ②
Ra1＝③
式中，θ＝30°.
由①②③式得
va＝④
(2)设粒子a在Ⅱ内做圆周运动的圆心为Oa，半径为Ra2，射出点为Pa(图中未画出轨迹)，∠P′OaPa＝θ′＝2θ.由洛伦兹力公式和牛顿第二定律得
qva(2B)＝m⑤
由①⑤式得
Ra2＝⑥
C、P′和Oa三点共线，且由⑥式知Oa点必位于x＝d的平面上，由对称性知，Pa点与P′点纵坐标相同，即yPa＝Ra1cosθ＋h⑦
式中，h是C点的y坐标．
设b在Ⅰ中运动的轨道半径为Rb1，由洛伦兹力公式和牛顿第二定律得
qB＝2⑧
设a到达Pa点时，b位于Pb点，转过的角度为α.如果b没有飞出Ⅰ，则
＝⑨
＝⑩
式中，t是a在区域Ⅱ中运动的时间，而
Ta2＝
Tb1＝
由⑤⑧⑨⑩式得α＝30°
由①③⑧式可见，b没有飞出Ⅰ.Pb点的y坐标为
yPb＝Rb1cosα＋Ra1－Rb1＋h
由①③⑦⑧式及题给条件得，a、b两粒子的y坐标之差为yPa－yPb＝(－2)d

本题难度：一般

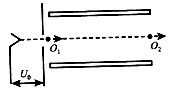
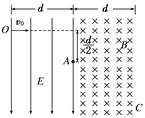
2、计算题  两块水平放置的平行金属板相距为d，板的长度L=d，如图所示，大量电子（已知电子质量为m、电荷量为e）由静止开始，经电压为U0的电场加速后。连续不断地从两板正中间以速度v0沿水平方向射入两板间，当两板间不加电场和磁场时，电子沿O1～O2轴线做直线运动。在两板间加上垂直于纸面向里，大小为的间断式周期性变化的磁场后，有些电子能从O2点水平射出磁场，有些电子则不能，为使电子从O2点水平射出，同时还要满足；
（1）电子在两板间必须做曲线运动，而不是直线运动；
（2）电子的运动轨迹能相交不能重叠，求所加磁场的最大周期Tmax与T关系和最小周期Tmin与T0的关系。

参考答案：解：由题给条件可得电子在磁场中转动半径为R=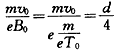

若在电子刚到达O1加磁场，电子将从下极板的左端水平飞出磁场，
为保证电子不从两极板左则飞出磁场，又要保证水平地从O2点射出，
电子在两板间水平向右运动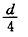后加上磁场，也就是电子在两板间水平向右运动T。
后加上磁场，电子先做d/4的直线运动，后做一个完整的圆周运动，再连续做三个周期后，
沿直线O1～O2，从点O2水平射出。
设电子做直线运动时间为
做圆周运动的时间为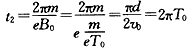
电子的运动轨迹如图甲所示，

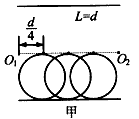
所加磁场的变化周期为 Tmin=t1+t2=(l+2π)T。
若电子在两板问水平向右运动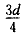后加L磁场，也就是电子在两板间水平向右运动3T。
后加上磁场，电子先做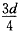的直线运动，后做一个完整的圆周运动，
这样电子可以从O2点水平射出设电子做直线运动时间为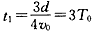
做圆周运动的时间为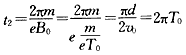
所加磁场的变化周期为Tmax=(3+2π)T。
电子的运动轨迹如图乙。

本题解析：

本题难度：困难

3、简答题  一个运动电荷通过某一空间时，没有发生偏转，那么这个空间是否存在电场或磁场，下列说法正确的是（　　）
A．一定不存在电场
B．一定不存在磁场
C．一定存在磁场
D．可能既存在磁场，又存在电场

参考答案：一个运动电荷通过某一空间时，没有发生偏转，可能存在电场：受到电场力，其方向与运动电荷的运动方向在同一条直线上；也可能存在磁场，不过磁场方向与运动电荷的速度方向在同一条直线上．所以可能存在磁场，也可能存在电场．故A、B、C、均错误．只有D正确
故选：D

本题解析：

本题难度：一般

4、计算题  （22分）如图甲所示，在xOy坐标平面的第一象限（包括x、y轴）内存在磁感应强度大小为B0、方向垂直于xOy平面且随时间做周期性变化的匀强磁场，如图乙所示，规定垂直xOy平面向里的磁场方向为正。在y轴左侧有一对竖直放置的平行金属板M、N，两板间的电势差为U0。一质量为m、电量为q的带正电粒子（重力和空气阻力均忽略不计），从贴近M板的中点无初速释放，通过N板小孔后从坐标原点O以某一速度沿x轴正方向垂直射入磁场中，经过一个磁场变化周期T0（T0未知）后到达第一象限内的某点P，此时粒子的速度方向恰好沿x轴正方向。

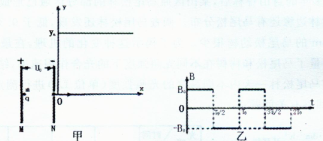
（1）求粒子进入磁场作匀速圆周运动时的运动半径；
（2）若粒子在t=0时刻从O点射入磁场中，求粒子在P点纵坐标的最大值ym及相应的磁场变化周期T0的值；
（3）若在上述（2）中，第一象限内y=ym处平行x轴放置有一屏幕，如图甲，磁场变化周期为上述（2）中T0，但M、N两板间的电势差U可以在U0<U<9U0范围内变化，粒子仍在t=0时刻从O点射入磁场中，求粒子可能击中的屏幕范围。

参考答案：解：（1）设粒子被电场加速获得速度大小为v0，根据动能定理qU0=mv02
解得：v0=.
带电粒子垂直进入匀强磁场后做半径为r的匀速圆周运动，q v0B0=m，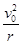
解得r=。
（2）设带电粒子在磁场中运动周期为T，则有T==。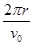
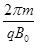如图所示，粒子在P点y坐标值最大，据几何知识有，OO1=PO2=r，
O1O2=2r，则AO1=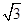r。
P点纵坐标最大值ym= OO1 +AO1+PO2=(2+).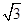
由几何关系知α=60°，粒子运动时转过α+90°=150°，磁场开始改变方向，即磁场变化半个周期内粒子运动转过150°角，则=T=.
（3）由U0≤U≤9 U0可得粒子速度v0≤v≤3 v0。
粒子在磁场中运动半径：r≤R≤3r。
由几何关系可得，在屏幕上击中的屏幕范围最左端轨迹如图2所示，该点横坐标x1=0；
由几何关系可得，在屏幕上击中的屏幕范围最右端轨迹如图3所示，
由(ym- Rm)2+x22=Rm2
解得该点横坐标x2=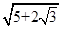r=；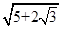
粒子可能击中的屏幕范围为：0≤x≤。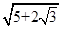

本题解析：应用动能定理、洛伦兹力公式、牛顿运动定律及其相关知识列方程解答。

本题难度：一般

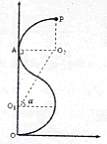
5、计算题  (14分)如图12所示，匀强电场区域和匀强磁场区域是紧邻的，且宽度相等均为d，电场方向在纸平面内竖直向下，而磁场方向垂直于纸面向里，一带正电的粒子从O点以速度v0沿垂直电场方向进入电场，从A点出电场进入磁场，离开电场时带电粒子在电场方向的偏转位移为电场宽度的一半，当粒子从磁场右边界上C点穿出磁场时速度方向与进入电场O点时的速度方向一致，已知d、v0(带电粒子重力不计)，求：

(1)粒子从C点穿出磁场时的速度大小v；
(2)电场强度E和磁感应强度B的比值.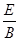

参考答案：(1) 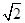v0　(2)v0

本题解析：(1)粒子在电场中偏转时做类平抛运动，则
垂直电场方向d＝v0t，平行电场方向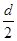＝t
得vy＝v0，到A点速度为v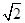＝v0
在磁场中速度大小不变，
所以从C点出磁场时速度大小仍为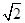v0
(2)在电场中偏转时，出A点时速度与水平方向成45°
vy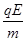＝t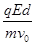＝，并且vy＝v0
得E＝

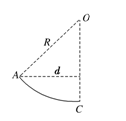
在磁场中做匀速圆周运动，如图所示
由几何关系得R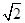＝d
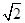又qvB＝，且v＝v0
得B＝
解得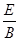＝v0.

本题难度：简单