1、计算题  如图所示，在区域Ⅰ(0≤x≤d)和区域Ⅱ(d≤x≤2d)内分别存在匀强磁场，磁感应强度大小分别为B和2B，方向相反，且都垂直于Oxy平面．一质量为m、带电荷量q(q＞0)的粒子a于某时刻从y轴上的P点射入区域Ⅰ，其速度方向沿x轴正向．已知a在离开区域Ⅰ时，速度方向与x轴正向的夹角为30°；此时，另一质量和电荷量均与a相同的粒子b也从P点沿x轴正向射入区域Ⅰ，其速度大小是a的；不计重力和两粒子之间的相互作用力．求：

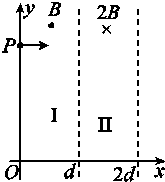
小题1:粒子a射入区域Ⅰ时速度的大小；
小题2:当a离开区域Ⅱ时，a、b两粒子的y坐标之差．

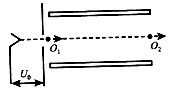
2、计算题  两块水平放置的平行金属板相距为d，板的长度L=d，如图所示，大量电子（已知电子质量为m、电荷量为e）由静止开始，经电压为U0的电场加速后。连续不断地从两板正中间以速度v0沿水平方向射入两板间，当两板间不加电场和磁场时，电子沿O1～O2轴线做直线运动。在两板间加上垂直于纸面向里，大小为的间断式周期性变化的磁场后，有些电子能从O2点水平射出磁场，有些电子则不能，为使电子从O2点水平射出，同时还要满足；
（1）电子在两板间必须做曲线运动，而不是直线运动；
（2）电子的运动轨迹能相交不能重叠，求所加磁场的最大周期Tmax与T关系和最小周期Tmin与T0的关系。

3、简答题  一个运动电荷通过某一空间时，没有发生偏转，那么这个空间是否存在电场或磁场，下列说法正确的是（　　）
A．一定不存在电场
B．一定不存在磁场
C．一定存在磁场
D．可能既存在磁场，又存在电场

4、计算题  （22分）如图甲所示，在xOy坐标平面的第一象限（包括x、y轴）内存在磁感应强度大小为B0、方向垂直于xOy平面且随时间做周期性变化的匀强磁场，如图乙所示，规定垂直xOy平面向里的磁场方向为正。在y轴左侧有一对竖直放置的平行金属板M、N，两板间的电势差为U0。一质量为m、电量为q的带正电粒子（重力和空气阻力均忽略不计），从贴近M板的中点无初速释放，通过N板小孔后从坐标原点O以某一速度沿x轴正方向垂直射入磁场中，经过一个磁场变化周期T0（T0未知）后到达第一象限内的某点P，此时粒子的速度方向恰好沿x轴正方向。

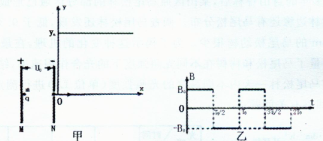
（1）求粒子进入磁场作匀速圆周运动时的运动半径；
（2）若粒子在t=0时刻从O点射入磁场中，求粒子在P点纵坐标的最大值ym及相应的磁场变化周期T0的值；
（3）若在上述（2）中，第一象限内y=ym处平行x轴放置有一屏幕，如图甲，磁场变化周期为上述（2）中T0，但M、N两板间的电势差U可以在U0<U<9U0范围内变化，粒子仍在t=0时刻从O点射入磁场中，求粒子可能击中的屏幕范围。

5、计算题  (14分)如图12所示，匀强电场区域和匀强磁场区域是紧邻的，且宽度相等均为d，电场方向在纸平面内竖直向下，而磁场方向垂直于纸面向里，一带正电的粒子从O点以速度v0沿垂直电场方向进入电场，从A点出电场进入磁场，离开电场时带电粒子在电场方向的偏转位移为电场宽度的一半，当粒子从磁场右边界上C点穿出磁场时速度方向与进入电场O点时的速度方向一致，已知d、v0(带电粒子重力不计)，求：

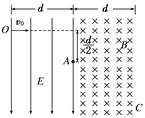
(1)粒子从C点穿出磁场时的速度大小v；
(2)电场强度E和磁感应强度B的比值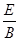.