1、填空题  如图所示，一块均匀木板AB，长为12m，重为200N，距A端3m处有一固定转动轴O，另一端B以绳悬住，使板呈水平状态，绳与木板的夹角为30°。如果绳能承受的最大拉力为200N，现使一个重600N的人在板上行走，则此人在距A端__________m至__________m的范围内是安全的。

参考答案：2,3.5

本题解析：当人在O点左侧行走时，当板恰好要逆时针转动时，人走到离O点向左最远处．此时绳子的拉力为零．
当人在O点右侧行走时，当绳拉力达到最大拉力时，人走到离O点向右最远处．根据力矩平衡条件求解人在板行走的安全距离．
解：当人在O点左侧行走时，当板恰好要逆时针转动时，设人走到离O点左侧距离xm处．
根据力矩平衡条件得：G人x=G板L，L=3m，得到x=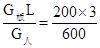m=1m，则人距A端距离为3m．
当人在O点右侧行走时，当绳拉力达到最大拉力时，人走到离O点向右最远处，设离A端距离为y．
G板L+G人（y-3）=F?OBsin30°? F=200N，OB=9m，L=3m
代入解得y=3.5m．
故本题答案是：2；3.5

本题难度：一般

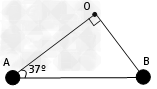
2、计算题  如图所示，OAB是一刚性轻质直角三角形支架，边长AB=0.2m，∠OAB=37°；在A、B两顶角处各固定一个大小不计的小球，质量均为1kg。支架可绕过O的水平轴在竖直平面内无摩擦地转动。（sin37°=0.6，cos37°=0.8，重力加速度g取10m/s2）
（1）为使支架静止时AB边水平，求在支架上施加的最小力；
（2）若将支架从AB位于水平位置开始由静止释放，求支架转动过程中A处小球速度的最大值。

参考答案：解：（1）施加的最小力满足的条件是：力臂最大
所以该力的作用在A点，方向垂直于OA向上
mg·OA·cos37°= mg·OB·cos53°+Fmin·OA
OA=0.16m，OB=0.12m，可解得Fmin=3.5N
作用在A点，在支架平面内垂直于OA向上
（2）支架力矩平衡时两小球的速度最大
设平衡时OA边与竖直方向夹角为θ
则有mg·OA·sinθ=mg·OB·sin（90°-θ），可得θ=37°
mg（OAcos37°-OAcos53°）-mg（OBcos37°-OBcos53°）=m（v12+ v22）
v1:v2= OA:OB=4:3
由上述两式可解得v1=0.32m/s

本题解析：

本题难度：一般

3、简答题  在用力矩盘做“有固定转动轴物体的平衡”的实验时，在用细线悬挂钩码前，以下哪些措施是必要的______．
A．判断力矩盘是否处于竖直平面．
B．判断横杆是否严格保持水平．
C．判断力矩盘与转轴间的摩擦是否足够小．
D．判断力矩盘的重心是否位于盘的中心．

参考答案：A、为了防止细线及弹簧称与力矩盘产生摩擦，判断力矩盘是否处在竖直平面是必要的．故A正确．
B、本实验与横杆MN是否平衡无关，没有必要检查横杆MN是否严格保持水平．故B错误．
C、D本实验要研究力矩盘平衡时砝码的拉力力矩和弹簧拉力力矩的关系，重力、摩擦力等影响要尽可能小，所以摩擦力要足够小，力矩盘的重心应在盘中心．故CD正确．
故选ACD

本题解析：

本题难度：一般

4、简答题  静止在水平地面上的粗细均匀的木棒长为L，质量为M，可绕固定转轴O自由转动．现用一始终垂直棒的作用力F作用于棒的一端，将木棒缓慢拉至竖直位置．则在拉起过程中，拉力F做的功为多少？
下面是某同学的
棒在拉力F作用下转过1/4圆弧，
故F做的功W=F×2πL/4=FπL/2
你认为上述解法是否正确？若正确，
请说明理由；若错误，请给出正确结果，并说明理由．

参考答案：上述解法不正确．
?因为棒在缓慢拉动过程中有力矩平衡．
由FL=MgL2COSθ?（θ为棒与水平面夹角）可知：
当θ逐渐增大，所以F逐渐减小，F是变力，不可直接用W=FS．
正确解法：
利用动能定理，有?
WF-MgL2=0?
所以WF=MgL2
答：在拉起过程中，拉力F做的功为MgL2．

本题解析：

本题难度：一般

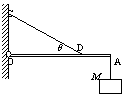
5、填空题  如图所示，一块质量M为7kg的物体悬挂在一根质量m为1kg、长L为2m的均匀直杆OA的A端处，杆可绕过O点且垂直于纸面的固定轴无摩擦地转动。一根细纲丝CD拉住这根杆，使它保持在水平位置，OD的长度l为1.5m，细纲丝与杆的夹角θ为30°，则杆所受到的顺时针力矩有_________个，钢丝对杆的拉力大小为_________N（重力加速度g＝10m/s2）。

参考答案：2，200

本题解析：

本题难度：一般