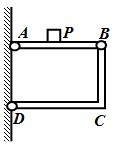
1、简答题  某课外兴趣小组为研究感应器设计了如图所示的装置，光滑导轨MN、PQ倾斜固定，与足够长水平固定的光滑导轨MR、PS在M、P两点光滑连接，水平导轨处在竖直方向的匀强磁场中，在水平导轨两侧安装有“感应控制器”，其结构中包括感应器1、感应器2和锁定控制器，现将导体棒A垂直导轨放置在水平导轨上，并置于锁定控制器处，导体棒B 垂直放置在倾斜导轨某处，由静止释放，当导体棒B到达MP处时，被感应器1感应，并发送锁定信号到锁定控制器，瞬间锁定导体棒A，使其不得水平移动，当导体棒B运动到CD处时，被感应器2感应，并发送解锁信号到锁定控制器，瞬间解锁导体棒A，之后两导体棒在磁场中运动。如图所示，两导体棒的质量为ma=mb=2kg,磁场的感应强度为B=1T，MP CD间的距离为L0=1m,导轨宽L=1m,两导体棒的电阻为，导轨电阻不计，CD与AB间距离足够大，导体棒B释放的位置到水平导轨的高度H=0.8m，（g=10m/s2）求（计算结果保留两位有效数字）
小题1:（1）导体棒到达感应器2处时的速度大小。
小题2:（2）由于感应控制器的安装使系统多损失的机械能。

参考答案：
小题1:（1）3.0m/s
小题2:（2）1.2 J

本题解析：考查电磁感应和动量能量的综合应用。考查的知识点有；电磁感应现象，楞次定律，法拉第电磁感应定律，动量守恒，动量定理，机械能守恒，能量守恒；综合性强；虽然过程中没有显示用到楞次定律，但分析过程已经渗透对这一知识点的考查，属重点知识点和综合分析能力的考查，难度在0.4左右。
小题1:(1)解；导体棒B下滑的过程，由动能定理得　　
　　　?　设由MP到以CD历时为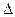t,则由法拉第电磁感应定律得
这一过程中的平均感应电动势大小为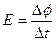　　
又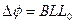　　　平均电流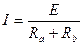　　　
对这一过程，由却是动量定理得，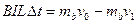
以上各式联立可得，导体棒b到达CD时的速度大小为v1=3.0m/s
小题2:　　导体棒a解除锁定后，两导体棒组成的系统动量守恒，设它们最终的共同速度大小为发v2
　　　　　　　　　　　　　得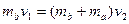　
　　　　　　　　　　若没有安装感应控制器，则导体棒B到达MP后，两导体棒组成的系统动量即守恒。
　　　　　　　　设这样可能达到的共同速度为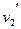，则有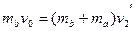　　
由能量守恒得　　由于安装感应控制器，使得系统多损失的机械能为
　
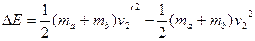
以上各式联立，并代入数据得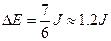

本题难度：一般

2、简答题  如图所示，一块质量为0.6kg均匀平板AB长0.8m，其左端搁在水平地面上，板与地面的夹角为370，板中心C垂直固定在轻支架上，支架长OC为0.3m，支架下端与水平固定转轴O连接．在平板A点处有一质量为0.5kg的小物体m以初速v0沿板向上运动，物体与平板间的动摩擦因数为0.2，g取10m/s2．试求：
（1）平板所受的重力的力矩；
（2）小物体运动到距B端多远恰能使平板翻转？
（3）若要保证平板不翻倒，给物体的初速度v0不能超过多大？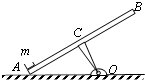

参考答案：（1）平板重力的力矩MG=mgLG=0.6×10×0.3×0.6N?m=1.08?N?m
（2）设物体距离C点的距离为X，根据力矩平衡有：MN+Mf=MG
? m1gX?cos37°+μm1gL?cos37°=MG?
? 代入数据，求得?X=0.21m
? 即距B端距离为0.4-0.21m=0.19?m
（3）滑行的最大距离为Sm=0.4+0.21m=0.61m
由动能定理得-m1gSmsin37°-μm1gSm?cos37°=-12m1v02
代入数据，求得v0=3.04m/s
答：（1）平板所受的重力的力矩为1.08N．m．
（2）小物体运动到距B端0.19m恰好使平板翻转．
（3）若要保证平板不翻倒，给物体的初速度v0不能超过3.04m/s．

本题解析：

本题难度：一般

3、实验题  如图所示为“研究有固定转动轴物体的平衡条件”实验，力矩盘上各同心圆的间距相等。在A、B两点分别用细线悬挂若干钩码，C点挂上弹簧秤后力矩盘平衡。已知每个钩码所受的重力均为1N。

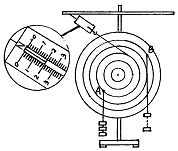
（1）此时弹簧秤示数为_____________N，B点细线上悬挂的钩码个数为_____________个；
（2）有同学在做这个实验时，发现顺时针力矩之和与逆时针力矩之和存在较大差距，检查发现读数和计算均无差错，请指出造成这种差距的一个可能原因，并提出简单的检验方法。（如例所示，将答案填在下表空格中）

参考答案：（1）2.0，3（2）

本题解析：

本题难度：一般

4、选择题  直杆AB和直角弯杆BCD按如图所示连接，A、B、D处均为铰链，杆及铰链的质量都不计．ABCD构成一长方形，将重力为G、可视为质点的物块放在图中P处．则（　　）
A．AB杆对BCD杆的作用力方向沿BC连线向下
B．BCD杆对AB杆的作用力方向沿DB连线斜向上
C．若AP间距变大，BCD杆对AB杆的作用力变大
D．若AP间距变大，AB杆对BCD杆的作用力对转动轴D的力矩不变