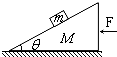
1、简答题 一个物体放在足够大的水平地面上,图甲中,若用水平变力拉动,其加速度随力变化图象为图乙所示.现从静止开始计时,改用图丙中周期性变化的水平力F作用(g取10m/s2).求:
(1)物体的质量及物体与地面间的动摩擦因数.
(2)求周期力作用下物体在一个周期内的位移大小.
(3)21s内力F对物体所做的功.
参考答案:(1)由牛顿第二定律得:F-μmg=ma
得:a=1mF-μg
结合乙图象得:m=4kg;μ=0.1
(2)0~2s:由牛顿第二定律可得F1-μmg=ma1
a1=F1-μmgm=12-44m/s2=2m/s2
前2s内通过的位移为x1=12a1t21=12×2×22m=4m
2s~4s:由牛顿第二定律可得F2-μmg=ma2
a2=F2-μmgm=-4-44m/s2=-2m/s2
2s~4s:物体做匀减速运动,t=4s时速度恰好为0,
由以上式可知:一个周期内的位移为x=2x1=8m
(3)20s即5个周期通过的位移x10=5×8=40m
第21秒通过的位移x′=12a1t′2=12×2×12m=1m
前21秒物体运动时拉力F做的功W=5(F1×s1+F2×s1)+F1×x′=5×[12×4+(-4)×4]+12×1J=172J
答:(1)物体的质量为4kg,物体与地面间的动摩擦因数为0.1.(2)求周期力作用下物体在一个周期内的位移大小为8m.(3)21s内力F对物体所做的功为172J
本题解析:
本题难度:一般
2、计算题 如图所示,厚度不计的薄板A长L=5.0m,质量M=5.0kg,放在水平桌面上。在A上距右端s=3.0m处放一物体B(大小不计),其质量m=2.0kg,已知A、B间的动摩擦因数μ=0.1,A与桌面间的动摩擦因数μ=0.2,原来系统静止。现在在板的右端施加一大小一定的水平力F=26N,持续作用在A上,将A从B下抽出。(g=10m/s2)求:
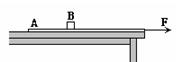
(1)A从B下抽出前A、B的加速度各是多少;
(2)B运动多长时间离开A.
参考答案:(1)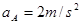 ,
, (2)
(2)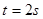
本题解析:(1)对于A: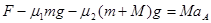 ?①
?①
解得?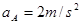 ?②
?②
对于B: 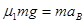 ?③
?③
解得? ?④
?④
(2)设经时间t抽出?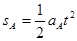 ?⑤
?⑤
 ?⑥
?⑥
 ?⑦
?⑦
 ?⑧
?⑧
点评:在应用牛顿第二定律时,加速度是连接力和运动的桥梁
本题难度:一般
3、简答题 如图,足够长的水平传送带始终以大小为v=3m/s的速度向左运动,传送带上有一质量为M=2kg的小木盒A,A与传送带之间的动摩擦因数为μ=0.3,开始时,A与传送带之间保持相对静止.先后相隔△t=3s有两个光滑的质量为m=1kg的小球B自传送带的左端出发,以v0=15m/s的速度在传送带上向右运动.第1个球与木盒相遇后,球立即进入盒中与盒保持相对静止,第2个球出发后历时△t1=1s/3而与木盒相遇.求(取g=10m/s2)
(1)第1个球与木盒相遇后瞬间,两者共同运动的速度时多大?
(2)第1个球出发后经过多长时间与木盒相遇?
(3)自木盒与第1个球相遇至与第2个球相遇的过程中,由于木盒与传送带间的摩擦而产生的热量是多少?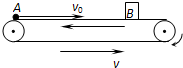
参考答案:(1)设第1个球与木盒相遇后瞬间,两者共同运动的速度为v1,根据动量守恒定律:mv0-Mv=(m+M)v1
代入数据,解得:v1=3m/s
(2)设第1个球与木盒的相遇点离传送带左端的距离为s,第1个球经过t0与木盒相遇,
则:t0=sv0
设第1个球进入木盒后两者共同运动的加速度为a,根据牛顿第二定律:μ(m+M)g=(m+M)a得:a=μg=3m/s2
设木盒减速运动的时间为t1,加速到与传送带相同的速度的时间为t2,则:t1=t2=△va=1s
故木盒在2s内的位移为零
依题意:s=v0△t1+v(△t+△t1-t1-t2-t0)
代入数据,解得:s=7.5m?t0=0.5s
(3)自木盒与第1个球相遇至与第2个球相遇的这一过程中,传送带的位移为S,木盒的位移为s1,则:S=v(△t+△t1-t0)=8.5ms1=v(△t+△t1-t1-t2-t0)=2.5m
故木盒相对与传送带的位移:△s=S-s1=6m
则木盒与传送带间的摩擦而产生的热量是:Q=f△s=54J
答:(1)第1个球与木盒相遇后瞬间,两者共同运动的速度为3m/s;
(2)第1个球出发后经过0.5s与木盒相遇;
(3)自木盒与第1个球相遇至与第2个球相遇的过程中,由于木盒与传送带间的摩擦而产生的热量为54J.
本题解析:
本题难度:一般
4、计算题 如图所示,在倾角θ=37°的足够长的固定斜面上,有一质量m=1kg的物体,物体与斜面间动摩擦因数μ=0.2。物体受到沿平行于斜面向上的轻细线的拉力F="9.6" N的作用,从静止开始运动,经2s绳子突然断了。求绳断后多长时间物体速度大小为22m/s。(结果保留两位有效数字,已知sin37°=0.6,g取10m/s2)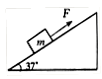
参考答案:5.5s
本题解析:第一阶段:在最初2 s内,物体在F=9.6N的拉力作用下,从静止开始沿斜面做匀加速运动,受力如图所示,有:沿斜面方向F-mgsinθ-Ff=ma1?…………(1分)
沿垂直斜面方向FN="mgcosθ?" …………(1分)
且Ff=μFN?…………(1分)
由①②③得:a1=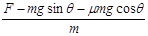 =2m/s2?…………(1分)
=2m/s2?…………(1分)
2 s末绳断时瞬时速度v1=a1t1="4" m/s?…………(1分)
第二阶段:从撤去F到物体继续沿斜面向上运动到达速度为零的过程,设加速度为a2,则:
a2=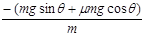 ="-7.6" m/s2?…………(3分)
="-7.6" m/s2?…………(3分)
设从断绳到物体达最高点所需时间为t2,据运动学公式v2=v1+a2t2,得t2="=0.53" s?…………(2分)
第三阶段:物体从最高点沿斜面下滑,在第三阶段物体加速度为a3,所需时间为t3.由牛顿定律知:
a3="(mgsinθ-μmgcosθ)/m=4.4" m/s2?…………(3分)
速度达v3="22" m/s,所需时间t3=(v3-0)/a3="5s?" …………(1分)
综上所述,从绳断到速度为22m/s所经历的总时间t=t2+t3=0.53s+5s≈5.5s
本题难度:一般
5、选择题 如图所示,质量为M、倾角为θ的斜面放在水平面上,在水平恒力F的作用下,斜面和质量为m的物体一起向左做匀加速运动,则此过程中斜面对物体的作用力的方向与竖直方向的夹角α是( )
A.可能α=0
B.可能向左上方,α≤θ
C.可能向左上方,α>θ
D.可能向右上方,α>θ