1、简答题  如图所示，ABCDEF是一边长为L的正六边形盒，各边均为绝缘板，盒外有方向垂直纸面向里、范围足够大的匀强磁场，磁感应强度大小为B．在盒内有两个与AF边平行的金属板M、N，且金属板N靠近盒子的中心O点，金属板M和盒子AF边的中点均开有小孔，两小孔与O点在同一直线上．现在O点静止放置一质量为m、电荷量为q的带正电粒子（不计粒子的重力）．
（1）如果在金属板N、M间加上电压UNM=U0时，粒子从AF边小孔射出后直接打在A点，试求电压U0的大小．
（2）如果改变金属板N、M间所加电压，试判断粒子从AF边小孔射出后能否直接打在C点．若不能，说明理由；若能，请求出此时电压UNM的大小．
（3）如果给金属板N、M间加一合适的电压，粒子从AF边小孔射出后恰好能以最短时间回到该小孔（粒子打在盒子各边时都不损失动能），试求最短时间．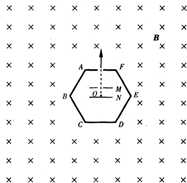

参考答案：（1）依题意，R=L4，
由qvB=mv2R，
及qU0=12mv02，
解得U0=qB2L232m
（2）设AF中点为G，连接GC，作其垂直平分线，与AF延长线交点即为圆心
由相似三角形得R′=O′G=13L4，
由牛顿第二定律，qvB=mv2R′，
∵qU0=12mv02，
∴UNM=169qB2L232m
（3）由于粒子在磁场中运动周期T=2πmqB，T与速率无关粒子撞击BC中点和DE中点后回到G，
用时最短圆周半径R″=32L，
得到最短时间t=300360T×3=5πmqB
答：（1）如果在金属板N、M间加上电压UNM=U0时，粒子从AF边小孔射出后直接打在A点，则电压U0的大小UqB2L232m．
（2）如果改变金属板N、M间所加电压，试判断粒子从AF边小孔射出后能否直接打在C点．若不能，说明理由；若能，此时电压UNM的大小169qB2L232m．
（3）如果给金属板N、M间加一合适的电压，粒子从AF边小孔射出后恰好能以最短时间回到该小孔，则最短时间为5πmqB．

本题解析：

本题难度：一般

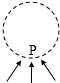
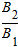2、选择题  如图，圆形区域内有一垂直纸面的匀强磁场，P为磁场边界上的一点．有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以同样的速率通过P?点进入磁场．这些粒子射出边界的位置均处于边界的某一段弧上，这段圆弧的弧长是圆周长的．将磁感应强度的大小从原来的B1?变为?B2，结果相应的弧长变为原来的一半，则等于（　　）

A．2
B．3
C．
D.