1、计算题  如图所示，空间某平面内有一条折线是磁场的分界线，在折线的两侧分布着方向相反、与平面垂直的匀强磁场，磁感应强度大小都为B。折线的顶角∠A＝90°，P、Q是折线上的两点，AP=AQ=L。现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出，不计微粒的重力。

（1）为使微粒从P点射出后，途经折线的顶点A而到达Q点，求初速度v应满足什么条件？
（2）求第（1）问中微粒从P点到达Q点所用的时间。

2、选择题  如图所示，竖直放置的两块很大的平行金属板a、b，相距为d，ab间的电场强度为E，今有一带正电的微粒从a板下边缘以初速度v0竖直向上射入电场，当它飞到b板时，速度大小不变，而方向变成水平方向，且刚好从高度也为d的狭缝穿过b板而进入bc区域，bc宽度也为d，所加电场大小为E，方向竖直向上，磁感应强度方向垂直于纸面向里，磁感应强度大小等于

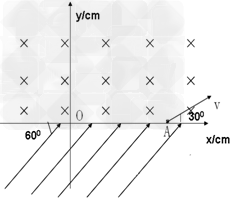
3、计算题  在如图所示的空间区域里，x轴下方有一匀强电场，场强方向跟x轴负方向成60°角，大小为E=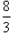×105N/C，x轴上方有一垂直纸面向里的匀强磁场，有一质子以速度v=2.0×106m/s由x轴上A点（OA=20cm）从与x轴正方向成30°角射入磁场，恰好从坐标原点O穿过x轴射入电场，已知质子质量m=1.6×10-27 kg，求
（1）匀强磁场的磁感应强度；
（2）质子经过电场后，再次射入磁场的位置和方向．

4、计算题  （１４分）如左图所示，x≥0的区域内有如右图所示大小不变、方向随时间周期性变化的磁场，磁场方向垂直纸面向外时为正方向。现有一质量为m、带电量为q的正电粒子，在t=0时刻从坐标原点O以速度v沿着与x轴正方向成75°角射入。粒子运动一段时间到达P点，P点坐标为(a,a),此时粒子的速度方向与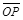延长线的夹角为30°.粒子在这过程中只受磁场力的作用。

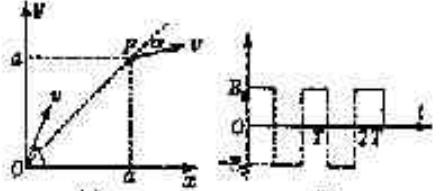
(1)若B为已知量,试求粒子在磁场中运动时的轨道半径R及周期T的表达式。
(2)说明在OP间运动的时间跟所加磁场的变化周期T之间应有什么样的关系才能使粒子完成上述运动。
(3)若B为未知量,那么所加磁场的变化周期T、磁感强度B0的大小各应满足什么条件，才能使粒子完成上述运动？(写出T及B0各应满足条件的表达式)

5、计算题  在xOy平面内有许多电子（质量为m、电量为e），从坐标O不断以相同速率v0沿不同方向射入第一象限，如图所示。现加一个垂直于xOy平面向内、磁感强度为B的匀强磁场，要求这些电子穿过磁场后都能平行于x轴向x轴正方向运动，求符合该条件磁场的最小面积。