1、计算题  （11分）如图所示，纸平面内一带电粒子以某一速度做直线运动，一段时间后进入一垂直于纸面向里的圆形匀强磁场区域（图中未画出磁场区域），粒子飞出磁场后从上板边缘平行于板面进入两面平行的金属板间，两金属板带等量异种电荷，粒子在两板间经偏转后恰从下板右边缘飞出。已知带电粒子的质量为m，电量为q，其重力不计，粒子进入磁场前的速度方向与带电板成θ=60°角。匀强磁场的磁感应强度为B，带电板板长为L，板间距为d，板间电压为U。试解答：

（1）上金属板带什么电？
（2）粒子刚进入金属板时速度为多大？
（3）圆形磁场区域的最小面积为多大？

参考答案：（1）上金属板带负电；（2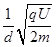）；（3）。

本题解析：（1）由于带电粒子在磁场中受到的洛伦兹力是向右下的，故由左手定则可知，粒子带负电，当它进入平行板间后受到向下电场力，故平行板的上金属板带负电；
（2）设带电粒子进入电场的初速度为v，在电场中偏转时有：d=?①
解得v=，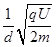

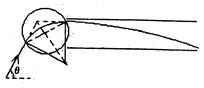
（3）如图所示，带电粒子在磁场中所受洛伦兹力作为向心力，设磁偏转的半径为R，圆形磁场区域的半径为r，则：qvB=m得R==；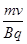
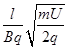由几何知识可得：r=Rsin30°
磁场区域的最小面积为S=πr2=。

本题难度：一般

2、选择题  (2010年高考江苏卷)如图所示，在匀强磁场中附加另一匀强磁场，附加磁场位于图中阴影区域，附加磁场区域的对称轴OO′与SS′垂直．a、b、c三个质子先后从S点沿垂直于磁场的方向射入磁场，它们的速度大小相等，b的速度方向与SS′垂直，a、c的速度方向与b的速度方向间的夹角分别为α、β，且α＞β.三个质子经过附加磁场区域后能到达同一点S′，则下列说法中正确的有(　　)

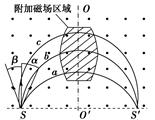
A三个质子从S运动到S′的时间相等
B．三个质子在附加磁场以外区域运动时，运动轨迹的圆心均在OO′轴上
C．若撤去附加磁场，a到达SS′连线上的位置距S点最近
D．附加磁场方向与原磁场方向相同

参考答案：CD

本题解析：洛伦兹力对粒子始终不做功，由于a、b、c三个质子射入磁场时的速度大小相等，所以它们进入磁场后速度大小始终不变，显然弧长最长的c运动时间最长，a运动时间最短，选项A错；撤去附加磁场后三个质子均做匀速圆周运动，其中质子b轨迹为半圆，由于α＞β，通过画图可看出a到达SS′连线上位置距S点最近，b到达SS′连线上的位置离S点最远，选项C正确；比较a、b两质点，b在附加磁场中运动的弧长比a在附加磁场中运动的弧长长，但它们均从同一位置S′离开磁场，故附加区域合磁场磁感应强度比原磁场磁感应强度大，因此附加磁场方向与原磁场方向相同，选项D正确．由于附加磁场区域的合磁场磁感应强度比原磁场的强，附加区域质子运动半径小，故未进入附加磁场之前的圆心位置在OO′轴右方，从附加磁场出来后的圆心在OO′左侧(如图)选项B错误．

本题难度：一般

3、计算题  在一真空室内存在着匀强电场和匀强磁场，电场与磁场的方向相同，已知电强E=40.0V/m，磁感应强度B=0.30T。如图所示，在该直空室内建立O－xyz三维直角坐标系，其中z轴竖直向上。质量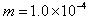kg、带负电的质点以速度v0=100m/s沿+x方向做匀速直线运动，速度方向与电场、磁场垂直，取g=10m/s2。
（1）求质点所受电场力与洛伦兹力大小之比；
（2）求带电质点的电荷量；
（3）若在质点通过O点时撤去磁场，求经过时间t=0.20s带电质点的位置坐标。

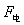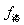参考答案：解：（1）电场力与洛伦兹力大小之比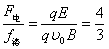
（2）电场力与场强方向相同，洛伦兹力与磁感应强度方向（即场强方向）垂直，带电质点受电场力和洛伦兹力的合力与重力平衡，故磁场和电场方向与yOz平面平行，与-y方向成53°斜向下，方向如图所示：?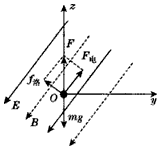
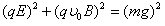
解得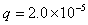C
（3）撤去磁场后，带电质点在沿x轴方向上做匀速直线运动，经过时间t=0.20s，沿x轴方向上的位移
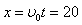m
带电质点受恒定合力，其大小等于洛伦兹力，方向与洛伦兹力方向相反，由几何关系可知质点受合力方向与+y方向成37°斜向下
质点的加速度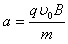=6.0m/s2
在t=0.20s内，沿此方向的位移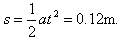
位移s在y轴方向的分量y=scos37°=9.6cm
在z轴方向的分量z=－ssin37°=－7.2cm
所以，经过时间t=0.2s带电质点的位置为 (20m，9.6cm，－7.2cm)

本题解析：

本题难度：困难

4、计算题  如图所示，Oxyz坐标系的y轴竖直向上，坐标系所在的空间存在匀强电场和匀强磁场，电场方向与x轴平行，从y轴上的M（0、H、0）点无初速释放一个质量为m、电荷量为q的带正电的小球，它落在xOy平面上的N（l、0、b）点（l>0， b>0）。若撤去磁场则小球落在xoz平面的P（l、0、b）点，已知重力加速度为g。
（1）已知磁场方向与某个坐标轴平行，请确定其可能的具体方向；
（2）求出电场强度的大小；
（3）求出小球落至N点时的速率。

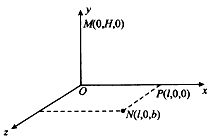
参考答案：解：（1）用左手定则判断出：磁场方向为x方向或y 方向
（2）在未加匀强磁场时，带电小球在电场力和重力作用下落到P点，设运动时间为t，小球自由下落，有H=gt2／2
小球沿x轴方向只受电场力作用，F=qE
小球沿x轴的位移为l=at2/2
小球沿x轴方向的加速度为a=F/m
联立求解，得E=mgl/qH
（3）带电小球在匀强磁场和匀强电场共存的区域运动时，洛伦兹力不做功，
电场力做功为：W=qEl
重力做功为WC=mgH
设落到N点时速度大小为v，根据动能定理得
?
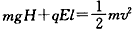解得。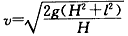

本题解析：

本题难度：困难

5、选择题  带电粒子以速度v沿CB方向射入一横截面为正方形的区域．C、B均为该正方形两边的中点，如图13所示，不计粒子的重力．当区域内有竖直方向的匀强电场E时，粒子从A点飞出，所用时间为t1；当区域内有垂直于纸面向里的磁感应强度为B的匀强磁场时，粒子也从A点飞出，所用时间为t2，下列说法正确的是(　　)

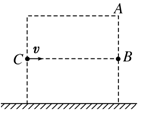
A．t1<t2?B．t1>t2?
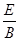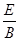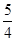C.＝v?D.＝v

参考答案：AD

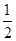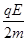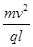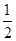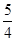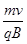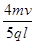本题解析：带电粒子在匀强电场中做类平抛运动，水平方向上做匀速运动，而在匀强磁场中做匀速圆周运动，水平方向上做减速运动，所以t2>t1，A项正确，B项错；设正方形区域的边长为l，则当加电场时，有l＝vt1和＝t12，得E＝.当加磁场时，根据几何关系，有(R－)2＋l2＝R2，得R＝l，再由R＝得B＝.所以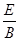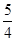＝v，D项对，C项错．

本题难度：简单