1、简答题
(1)AO的长度;
(2)两球碰撞过程损失的机械能;
(3)M每次与斜面的碰撞均没有机械能损失,且满足反射定律,则M从开始运动到第2次飞出磁场共用多少时间?
(4)若M第2次刚飞出磁场时即撤去电、磁场,求M落在斜面上的位置与O的距离。(用M碰后的速度V表示最终结果即可)
参考答案:(1)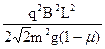 +L (2)
+L (2)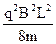
(3)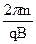 +
+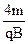 +
+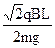 ?(4)
?(4)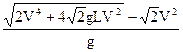
本题解析:(1)由题意可知,M在磁场中做匀速圆周运动,半径为R=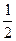 Lsinθ=
Lsinθ=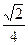 L….1分
L….1分
设碰撞后M的速度为V,由R=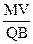 =
=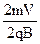 =
=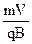 ,得
,得
V=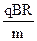 =
=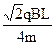 …………………………………………………………………..2分
…………………………………………………………………..2分
M与M碰撞过程系统水平方向合外力为0,故水平方向动量守恒,设m碰前速度 V0,有:? mV0="MV?" 得? V0=2V=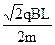 ………………………………………..2分
………………………………………..2分
M从A到C做初速度为0的匀加速运动,从C到O因为 qE=mg,故做匀速运动,
设AC=s,由动能定理有:
mgssinθ-μmgscosθ=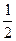 m
m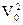 -0………………………………………….2分
-0………………………………………….2分
解得? s=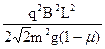 ……………………………………………………….2分
……………………………………………………….2分
所以? AO=s+L=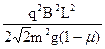 +L…………………………………………….1分
+L…………………………………………….1分
(2)ΔE=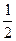 m
m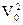 -
-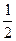 M
M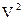 =
=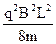 ………………………………………….2分
………………………………………….2分
(3)M做匀速圆周运动的周期T=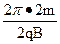 ?=
?=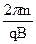 …………………………1分
…………………………1分
出磁场在电场中做匀速运动,时间为t1=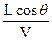 ……………………………...1分
……………………………...1分
与斜面碰撞后做竖直上抛运动,上升时间为t2=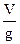 ……………………………1分
……………………………1分
所以总时间为t=T+2t1+2t2=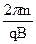 +
+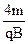 +
+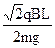 …………………….……….1分
…………………….……….1分
(4)撤去电、磁场后M做平抛运动,设落在斜面上的D点,DO=d,用时为tp,则有
dcosθ=VtP ……………………………………………………………….....1.分
2Lsinθ-dsinθ=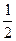 g
g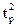 ……………………………………………………..1分
……………………………………………………..1分
解得d=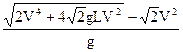 ……………………………………2分
……………………………………2分

本题难度:一般
2、计算题 如图所示,两平行的、间距为d的光滑金属导轨b1b2b3b4、c1c2c3c4分别固定在竖直平面内,整个导轨平滑连接,b2b3、c2c3位于同一水平面(规定该水平面的重力势能为零),其间有一边界为b2b3c3c2、方向竖直向上的匀强磁场,磁感应强度大小为B,导轨两端均连有电阻为R的白炽灯泡。一长为d的金属杆PN与两导轨接触良好,其质量为m、电阻为 。若金属杆从导轨左侧某一位置开始以初速度v0滑下,通过磁场区域后,再沿导轨右侧上滑至其初始位置高度一半时速度恰为零,此后金属杆做往复运动。金属杆第一次通过磁场区域的过程中,每个灯泡产生的热量为Q,重力加速度为g,除金属杆和灯泡外其余部分的电阻不计。求:
。若金属杆从导轨左侧某一位置开始以初速度v0滑下,通过磁场区域后,再沿导轨右侧上滑至其初始位置高度一半时速度恰为零,此后金属杆做往复运动。金属杆第一次通过磁场区域的过程中,每个灯泡产生的热量为Q,重力加速度为g,除金属杆和灯泡外其余部分的电阻不计。求:
(1)金属杆第一次通过磁场区域的过程中损失的机械能;
(2)金属杆初始位置的高度;
(3)金属杆第一次刚进入磁场区域时加速度的大小。
参考答案:(1)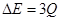 (2)
(2) (3)
(3)
本题解析:(1)设金属杆第一次通过磁场区域的过程损失的机械能为
灯泡的并联电阻为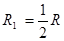 ? ①
? ①
回路的总电阻 ? ②
? ②
由焦耳定律得: ? ③
? ③
由①②③得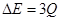 ? ④
? ④
(2)设金属杆开始下滑时的高度为h?
全程由能量转化和守恒定律有: ? ⑤
? ⑤
得: ? ⑥
? ⑥
(3)设金属杆第一次刚进入磁场区域时速度是v1 ,加速度为a,
金属杆刚进入磁场区域时产生的电动势为 ? ⑦
? ⑦
回路电流 ? ⑧
? ⑧
金属杆受到的安培力为 ? ⑨
? ⑨
由牛顿第二定律有: ? ⑩
? ⑩
由机械能守恒定律有: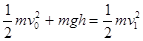 ? ⑾
? ⑾
联立②⑥⑦⑧⑨⑩⑾得 ? ⑿
? ⑿
本题难度:一般
3、选择题 在图中虚线所示的区域存在匀强电场和匀强磁场。一带电粒子沿x轴正方向进入此区域,在穿过此区域的过程中运动方向始终不发生偏转。不计重力的影响,电场强度E和磁感应强度B的方向可能是
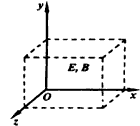
[? ]
A.E和B都沿y轴方向
B.E沿y轴正向,B沿z轴正向
C.E沿z轴正向,B沿y轴正向
D.E和B都沿z轴方向
参考答案:B
本题解析:
本题难度:一般
4、选择题 原来静止的质子经加速电压加速之后,垂直进入磁感应强度为B的匀强磁场中,做半径为r的匀速圆周运动,则下列叙述正确的是
[? ]
A.若半径r保持不变,加速电压U越大,则需要的磁感应强度B越大
B.若加速电压U保持不变,磁感应强度B越大,则半径r越大
C.若磁感应强度B保持不变,加速电压U越大,则半径r越小
D.若磁感应强度B保持不变,加速电压U越大,则质子做圆周运动的周期越大
参考答案:A
本题解析:
本题难度:一般
5、计算题 有一个带正电的小球,质量为m、电量为q,静止在固定的绝缘支架上.现设法给小球一个瞬时的初速度υ0使小求水平飞出,飞出时小球的电量没有改变.同一竖直面内,有一个竖直固定放置的圆环(圆环平面保持水平),环的直径略大于小球直径,如图所示.要使小球能准确进入圆环,可在空间分布匀强电场或匀强磁场(匀强电场和匀强磁场可单独存在,也可同时存在),请设计两种分布方式,并求出:
(1)相应的电场强度E或磁感应强度B的大小和方向;
(2)相应的小球到圆环的时间t .
(若加匀强电场,则匀强电场限制在竖直面内;若加匀强磁场,则匀强磁场限制在垂直纸面情况.已知υ0>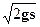 ,小球受重力不能忽略)
,小球受重力不能忽略)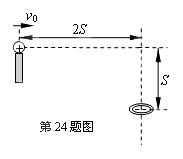
参考答案:
 方案2(11分):
方案2(11分):
加竖直向上匀强电场,在与圆环中心相距S处加垂直纸面向外的匀强磁场(如图所示)
(2分)
竖直方向? mg =qE

解得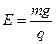 ?(2分)
?(2分)
带电小球从运动开始到进入磁场: t1=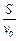 ?(1分)
?(1分)
进入磁场后带电小球在洛仑兹力作用下做圆周运动,
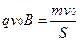 ?(2分)
?(2分)
得:?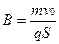 ?(1分)
?(1分)
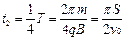 ?(2分)
?(2分)
小球到达圆环总时间t=t1+t2=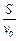 (1+
(1+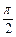 )?(1分)
)?(1分)
方案3:
加水平向左分布匀强电场E?(2分)
竖直方向自由落体运动: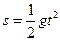 ?①?(1分)
?①?(1分)
水平方向做匀减速运动:2S =υ0t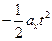 ?②?(2分)
?②?(2分)
qE=max?③?(2分)
解得?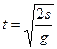 ?(2分)
?(2分)
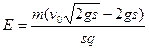 ?(2分)
?(2分)
说明:本题是开放性的题目,只要学生答题方案合理均给分
本题解析:略
本题难度:一般