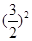1、计算题  两颗靠的较近的天体称为双星，它们以两者的连线上某点为圆心做匀速圆周运动，而不会由于万有引力作用，使它们吸在一起（不考虑其他天体对它们的影响），已知两天体质量分别为m1和m2，相距为L，求它们运转的角速度。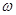

参考答案：ω=√G(m1+m2)/L3

本题解析：他们之间的相互作用力充当向心力，所以有：m1ω2r1=Gm1m2/L2（1）
m2ω2r2=Gm1m2/L2（2）
r1+r2= L（3）
联立三式可得ω=√G(m1+m2)/L3
点评：“双星”是万有引力部分常见的题型，关键抓住“双星”的条件：角速度相同、周期相同，采用隔离法由牛顿第二定律研究．

本题难度：一般

2、选择题  在地球赤道上，质量1 kg的物体随同地球自转需要的向心力最接近的数值为
[? ]
A．103 N　　
B．10 N
C．10-2 N　　
D．10-4 N

参考答案：C

本题解析：

本题难度：简单

3、计算题  17世纪初，开普勒提出的行星运动定律指出了行星运动的规律后，人们迫切想了解这一规律的本质，之后很多的学者提出各种观点，最终由牛顿的万用引力定律揭开了天体运动的神秘面纱。牛顿首先从太阳对行星的引力出发，凭借其运动三定律猜测行星之所以围绕太阳运转是因为其受到了太阳的引力，并导出了引力公式。牛顿的思想进一步解放，指出这一引力与使月球围绕地球运动的力、使苹果落地的力应遵循相同的规律，并给出了著名的“月-地检验”，为万有引力定律的得出提供了强有力的依据。“月-地检验”的基本思路可设置为以下两个问题，已知地球半径为6400km，月地距离约为地球半径的60倍，请再结合下面给出的已知量计算：（结果均保留三位有效数字）
（1）已知月球的公转周期为27.3天，据此求月球的向心加速度？
（2）已知地球表面的重力加速度为9.8m/s2，试据此求月球的向心加速度？

参考答案：（1）0.00272 ms-2
（2）0.00272 ms-2

本题解析：

本题难度：一般

4、选择题  北斗卫星导航系统（BDS）是中国自行研制的全球卫星导航系统，该系统将由35颗卫星组成，卫星的轨道有三种：地球同步轨道、中地球轨道和倾斜轨道。其中，同步轨道半径大约是中轨道半径的1．5倍，那么同步卫星与中轨道卫星的周期之比约为
A．
B．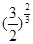
C．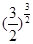
D．