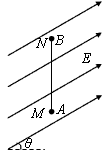
1、计算题  如图所示，一根长L＝1.5 m的光滑绝缘细直杆MN，竖直固定在场强为E＝1.0×105 N/C、与水平方向成θ＝30°角的倾斜向上的匀强电场中。杆的下端M固定一个带电小球A，电荷量Q＝+4.5×10－6 C；另一带电小球B穿在杆上可自由滑动，电荷量q＝+1.0×10一6 C，质量m＝1.0×10一2 kg。现将小球B从杆的上端N静止释放，小球B开始运动。（静电力常量k＝9.0×109 N·m2／C2，取g＝10 m/s2）
（1）小球B开始运动时的加速度为多大？
（2）小球B的速度最大时，距M端的高度h1为多大？
（3）小球B从N端运动到距M端的高度h2＝0.61 m时，速度为v＝1.0 m/s，求此过程中小球B的电势能改变了多少？

参考答案：解：（1）开始运动时小球B受重力、库仑力、杆的弹力和电场力，沿杆方向运动，由牛顿第二定律得：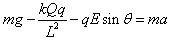
解得：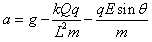
代入数据解得：a＝3.2 m/s2
（2）小球B速度最大时合力为零，即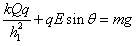
解得：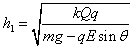
代入数据解得：h1＝0.9 m
（3）小球B从开始运动到速度为v的过程中，设重力做功为W1，电场力做功为W2，库仑力做功为W3，根据动能定理有：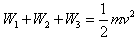


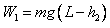
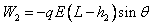
解得：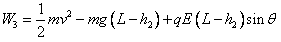
设小球B的电势能改变了△Ep，则：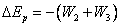

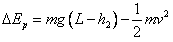
解得：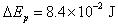

本题解析：

本题难度：困难

2、选择题  如图，在光滑水平面上放着紧靠在一起的A、B两物体，B的质量是A的2倍，Ｂ受到向右的恒力ＦB=2N，Ａ受到的水平力ＦA=(9-2t)N，(t的单位是s)。从t＝0开始计时，则

A.Ａ物体在3s末时刻的加速度是初始时刻的5／11倍；
B.t＞４s后B物体做匀加速直线运动；
C.t＝4.5s时A物体的速度为零；
D.t＞4.5s后，AB的加速度方向相反。

参考答案：ABD

本题解析：设A质量为1Kg，B质量为2Kg。3s末时FA=3N。假设AB之间没有相互作用，则A的加速度为3m/s2，B的加速度为1m/s2。说明AB之间没有分开。所以此刻加速度为5/3(m/s2)。在初始时刻整体加速度为11/5(m/s2)，所以A对。当A的加速度小于1m/s2时，AB分开，所以t＞４s后，B物体做匀加速直线运动，B对。由于AB一直加速，所以t＝4.5s时，Ａ物体的速度不等于零，C错。t＞4.5s后，AB的加速度方向相反，D对。
点评：本题考查了牛顿第二定律的瞬时性、方向性。

本题难度：简单

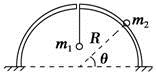
3、计算题  如图所示，半径为R的半球支撑面顶部有一小孔．质量分别为m1和m2的两只小球(视为质点)，通过一根穿过半球顶部小孔的细线相连，不计所有摩擦．请你分析：
(1)m2小球静止在球面上时，其平衡位置与半球面的球心连线跟水平方向的夹角为θ，则m1、m2、θ和R之间应满足什么关系；
(2)若m2小球静止于θ＝45°处，现将其沿半球面稍稍向下移动一些，则释放后m2能否回到
原来位置？
?

参考答案：(1)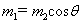与R无关? (2)不能　m2向下运动

本题解析：：（1）根据平衡条件有?对m2：m2gcosθ=T，对m1：T=m1g，所以m1=m2cosθ，与R无关．
（2）将m2沿半球面稍稍向下，不能回到原来位置，因为m2所受的合力为m2gcosθ′-m1g=m2g（cosθ′-cos 45°）＞0（因为θ′＜45°），所以m2将向下运动．

本题难度：简单

4、选择题  如图所示，水平地面上有两块完全相同的木块A、B，水平推力F作用在木块A上，用FAB表示木块A、B间的相互作用力，下列说法可能正确的是

[? ]
A．若地面是完全光滑的，则FAB＝F
B．若地面是完全光滑的，则FAB＝F/2
C．若地面是有摩擦的，且木块A、B未被推动，可能FAB＝F/3
D．若地面是有摩擦的，且木块A、B被推动，则FAB＝F/2

参考答案：BCD

本题解析：

本题难度：一般

5、选择题  如测图所示，在不计滑轮摩擦和绳子质量的条件下，当小车匀速向右运动时，物体A的受力情况是

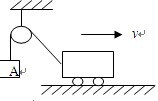
A．绳的拉力小于A的重力
B．绳的拉力等于A的重力
C．绳的拉力大于A的重力
D．绳的拉力先大于A的重力，后变为小于重力

参考答案：C

本题解析：：设和小车连接的绳子与水平面的夹角为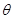，小车的速度为v，则这个速度分解为沿绳方向向下和垂直绳方向向上的速度，根据平行四边形法则解三角形得绳方向的 速度为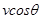，随着小车匀速向右运动，显然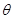逐渐减小，因为绳方向的速度越来越大，又知物体A的速度与绳子的速度大小一样，所以物体A向上做加速运动， 则由牛顿第二定律得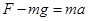：，即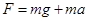，因此，绳的拉力大于物体A的重力，故选项C正确，选项ABD错误．
故选：C．
点评：在分析合运动与分运动时要明确物体实际运动为合运动，因此，判断小车的运动为合运动是关键，同时要根据运动的效果分解合运动．

本题难度：一般