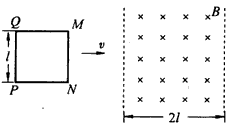
1、计算题  如图所示，用质量为m、电阻为R的均匀导线做成边长为l的单匝正方形线框MNPQ，线框每一边的电阻都相等，将线框置于光滑绝缘的水平面上，在线框的右侧存在竖直方向的有界匀强磁场，磁场边界间的距离为2l，磁感应强度为B。在垂直MN边的水平拉力作用下，线框以垂直磁场边界的速度v匀速穿过磁场，在运动过程中线框平面水平，且MN边与磁场的边界平行，求：
（1）线框MN边刚进入磁场时，线框中感应电流的大小；
（2）线框MN边刚进入磁场时，M、N两点间的电压UMN；
（3）在线框从MN边刚进入磁场到PQ边刚穿出磁场的过程中，水平拉力对线框所做的功W。

参考答案：解：（1）线框MN边在磁场中运动时，感应电动势E=Blv
线框中的感应电流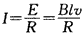
（2）M、N两点间的电压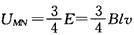
（3）只有MN边在磁场中时，线框运动的时间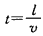
此过程线框中产生的焦耳热
只有PQ边在磁场中运动时线框中产生的焦耳热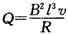
根据能量守恒定律得水平外力做功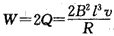

本题解析：

本题难度：一般

2、计算题  如图所示，将长为1m的导线从中间折成约106°的角，使其所在的平面垂直于磁感应强度为0.5T的匀强磁场。为使导线中产生4V的感应电动势，导线切割磁感线的最小速度约为多大？（sin53°=0.8）

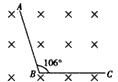
参考答案：解：当折导线切割磁感线有效长度最长时，即以AC来切割，速度最小
?
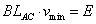得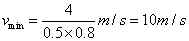

本题解析：

本题难度：一般

3、选择题  一段导线在磁场中做切割磁感线运动，下面说法正确的是（　　）
A．导体中一定有感应电动势
B．导体中一定有感应电流
C．导体一定受到与运动方向相反的磁场作用力
D．以上说法均不正确

参考答案：A

本题解析：

本题难度：一般

4、填空题  如图所示，垂直于纸面向里的匀强磁场，磁感应强度随时间的变化率为△B/△t=k（k为常量）．一边长为l的线框，其电阻为R，线框有一半面积处于磁场区域中．则线框中感应电流的功率为______；安培力随时间的变化率为______．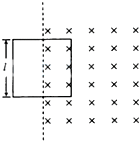

参考答案：（1）根据法拉第电磁感应定律得
? 感应电动势? E=△B△t?12L2=12kL2
由欧姆定律得感应电流的大小I=ER=kL22R
所以线框中感应电流的功率为P=I2R=(kL22R)2R=l4k24R
（2）磁场对方框作用力的大小F=BIL，B=B0+kt
则得到F=kl32R（B0+kt），
所以安培力随时间的变化率为?l3k22R．
故答案为：l4k24R；?l3k22R

本题解析：

本题难度：一般

5、简答题  如图所示，足够长的光滑平行导轨MN、PQ竖直放置，磁感应强度为B的匀强磁场垂直穿过导轨平面，导轨的M与P两端连接阻值为R=0.40Ω的电阻，质量为m=0.010kg，电阻r=0.30Ω的金属棒ab紧贴在导轨上．现使金属棒ab由静止开始下滑，其下滑距离与时间的关系如下表所示（不计导轨的电阻，取g=10m/s2）

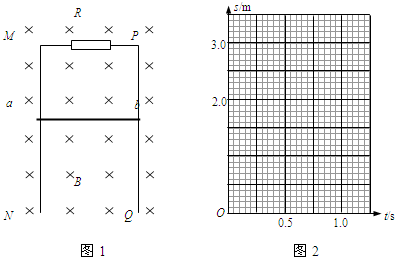
参考答案：

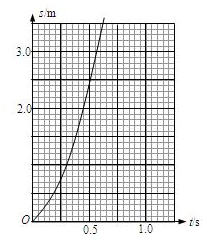
（1）0.7s内的位移-时间图象如图．
? （2）由图，金属棒在0.7s末的速度为
? v=△s△t=7m/s?
? 由题，金属棒ab下滑高度h=3.5m，设电路中产生的总热量为Q．
? 由能量守恒定律得? mgh=12mv2+Q
?又QR=I2Rt，Q=I2（R+r）t，得到
? QR=RR+rQ=0.06J
? （3）重力对金属棒做功的最大功率P=mgv=0.7W
答：（1）0.7s内的位移-时间图象如图．
? （2）金属棒ab在开始运动的0.7s内电阻R上产生的热量为0.06J．
? （3）重力对金属棒做功的最大功率P=mgv=0.7W．

本题解析：

本题难度：一般