1、简答题 如图所示,A、B为平行金属板,两板相距为d,接在电压为U的电源上,在A板的中央有一小孔M.今有一质量为m的带电质点,自A板上方相距为h的O点由静止自由下落,穿过小孔M后到达距B板
d的N点时速度恰好为零.若把A板向下平移d,带电质点仍从O点由静止自由下落.试求:
(1)带电质点的电荷量并指出带什么电.
(2)带电质点能否到达B板?若能,求出质点到达B板时的速度大小.若不能,求出质点速度为零的位置距B板的距离.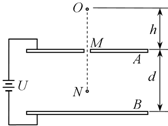
参考答案:(1)质点先做自由落体运动到M点,到达N孔时速度恰好为零,说明在MN间做减速运动,合外力向上,所以电场力方向向上,而电场强度方向向下,所以质点带负电,
根据动能定理得:
mgh(h+23d)-23qU=0-0
解得:q=mg(3h+2d)2U
(2)设质点速度为零的位置距离B板的距离为x,则根据动能定理得:
mg(h+d-x)-qd2-xd2U=0-0
解得:x=hd2(3h+d)
答:(1)带电质点的电荷量为mg(3h+2d)2U,带负电.
(2)带电质点不能到达B板,质点速度为零的位置距B板的距离为hd2(3h+d).
本题解析:
本题难度:一般
2、计算题 如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d。MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,其质量为m、电荷量为+q(可视为点电荷,不影响电场的分布),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v,已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g。求:
(1)C、O间的电势差UCO;
(2)小球p在O点时的加速度;
(3)小球p经过与点电荷B等高的D点时的速度。

参考答案:解:(1)小球p由C运动到O时,由动能定理得:
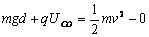
∴
(2)小球p经过O点时受力如图: 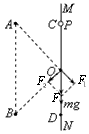 由库仑定律得:
由库仑定律得:
它们的合力为: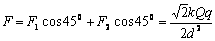
∴p在O点处的加速度: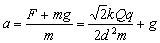 ,方向竖直向下
,方向竖直向下
(3)由电场特点可知,在C、D间电场的分布是对称的,即小球p由C运动到O与由O运动到D的过程中合外力做的功是相等的,运用动能定理

解得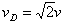
本题解析:
本题难度:困难
3、选择题 (7分)如图所示为固定在竖直平面内的光滑轨道ABCD,其中ABC部分为半径R=0.9m的半圆形轨道,CD部分为水平轨道。一个质量m="1" kg的小球沿水平方向进入轨道,通过最高点A时对轨道的压力为其重力的3倍。小球运动过程中所受空气阻力忽略不计,g取10m/s2。

(1)画出小球在A点时的受力示意图:
(2)求出小球在A点时的速度大小v ;
;
(3)求出小球经过C点进入半圆形轨道时对轨道的压力N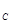 。
。
参考答案:(1)A点受力分析如下图 (2)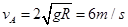 ?(3)
?(3)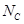 =90N?
=90N?

本题解析:A点受力重力mg方向竖直向下,轨道最高点对小球压力F=3mg,方向竖直向下。合力提供向心力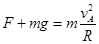 ,则有
,则有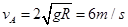 。从C到A点,光滑轨道,只有重力做功,根据动能定理
。从C到A点,光滑轨道,只有重力做功,根据动能定理 ,带入数据得
,带入数据得 。C点受竖直向下的重力mg作用和竖直向上的支持力F,合力提供向心力
。C点受竖直向下的重力mg作用和竖直向上的支持力F,合力提供向心力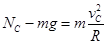 , 则有
, 则有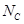 =90N。
=90N。
本题难度:一般
4、选择题 下列关于运动物体所受合外力做功和动能变化的关系正确的是( )
A.如果物体所受合外力为零,则合外力对物体做的功一定为零
B.如果合外力对物体所做的功为零,则合外力一定为零
C.物体在合外力作用下做变速运动,动能一定发生变化
D.物体的动能不变,所受合外力一定为零
参考答案:
A、如果物体所受合外力为零,根据功的公式W=Flcosα得知,合外力对物体做的功一定为零.故A正确.
B、如果合外力做的功为零,但合外力不一定为零,也可能物体的合外力和运动方向垂直而不做功,比如匀速圆周运动.故B错误.
C、物体做变速运动可能是速度方向变化而速度大小不变.所以,做变速运动的物体,动能可能不变,故C错误.
D、物体动能不变,根据动能定理得知,合外力不做功,但合外力不一定为零.故D错误.
故选A
本题解析:
本题难度:简单
5、计算题 如图所示,摩托车做腾跃特技表演,以1.0m/s的初速度沿曲面冲上高0.8m、顶部水平的高台,若摩托车冲上高台的过程中始终以额定功率1.8kW行驶,经过1.2s到达平台顶部,立即关闭油门,离开平台后,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑.A、B为圆弧两端点,圆弧的最低点B与水平传送带相切,传送带以v1=8m/s的速度匀速运动,传送带长为8.5m,摩托车轮胎与传送带间为滑动摩擦,动摩擦因数为μ=0.4。已知圆弧半径为R= m,AB所对应的圆心角为θ=53o,人和车的总质量为180kg,特技表演的过程中到达传送带之前不计一切阻力(计算中取g=10m/s2,
m,AB所对应的圆心角为θ=53o,人和车的总质量为180kg,特技表演的过程中到达传送带之前不计一切阻力(计算中取g=10m/s2,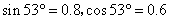 )。求:?
)。求:?
(1)人和车到达顶部平台时的速度v;
(2)从平台飞出到A点,人和车运动的水平距离s;
(3) 人和车运动到圆弧轨道最低点O时对轨道的压力;
(4) 人和车在传送带上的运动时间。
参考答案:(1)摩托车冲上高台的过程中,由动能定理得
 ?………………………………………………①
?………………………………………………①
代入数据解得
v=3m/s…………………………………………………………………………②
(2)摩托车离开平台后平抛运动过程中,在竖直方向
 ?……………………………………………………………………③
?……………………………………………………………………③
水平方向:
s=vt=1.2m………………………………………………………………………④
(3) 设人和车的最低点速度为vB,则摩托车由高台顶部到圆弧轨道最低点的过程中,
由机械能守恒定律得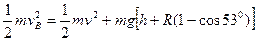 ……………………⑤
……………………⑤
得: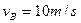
在最低点,据牛顿第二定律,有
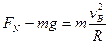 ?……………………………………………………………⑥
?……………………………………………………………⑥
代入数据解得

由牛顿第三定律可知,小孩对轨道的压力为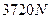 ?…………………………⑦
?…………………………⑦
(4)由牛顿第二定律得:
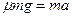 ……………………………………
…………………………………… ………………………………⑧
………………………………⑧
解得:
由运动学公式得:

解得: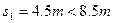 可知到达C点以前和传送带一起匀速运动。……⑨
可知到达C点以前和传送带一起匀速运动。……⑨
再由运动学公式,得:
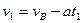 ?……………………………………………………………………⑩
?……………………………………………………………………⑩
解得: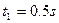
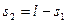 ?………………………………………………………………………⑾
?………………………………………………………………………⑾
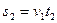 …………………………………………………………………………⑿
…………………………………………………………………………⑿
解得:
所以总时间为: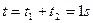 …………………………………………………⒀
…………………………………………………⒀
本题解析:略
本题难度:一般