1、选择题  已知地球质量是月球质量的a倍，地球半径是月球半径的b倍，下列结论中正确的是(? )
A．地球表面和月球表面的重力加速度之比为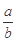
B．环绕地球表面和月球表面运行卫星的速率之比为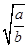
C．环绕地球表面和月球表面运行卫星的周期之比为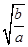
D．环绕地球表面和月球表面运行卫星的角速度之比为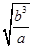

参考答案：B

本题解析：设星球的质量为M，半径为R，物体的质量为m，则在星球表面上，物体所受的重力近似等于星球的万有引力，则有，得星球表面的重力加速度，故地球表面和月球表面的重力加速度之比为，A错；卫星绕星球圆周时，星球对卫星的万有引力等于卫星的向心力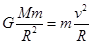，，得绕星球表面运行的卫星速度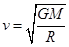，得环绕地球表面和月球表面运行卫星的速度之比为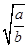?，B正确；绕星球表面运行的卫星周期为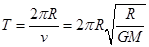，得环绕地球表面和月球表面运行卫星的周期之比为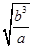，C错；绕星球表面运行的卫星角速度为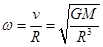，得环绕地球表面和月球表面运行卫星的角速度之比为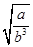，D错，所以本题选择B。

本题难度：一般

2、选择题  “探月热”方兴未艾，我国研制的月球卫星“嫦娥二号”已发射升空，已知月球质量为M，半径为R．引力常量为G，以下说法可能的是?（?）
A．在月球上以初速度v0竖直上抛一个物体，物体上升的最大高度为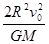
B．在月球上以初速度v0竖直上抛一个物体，物体落回到抛出点所用时间为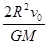
C．在月球上发射一颗绕它沿圆形轨道运行的卫星的最大运行速度为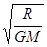
D．在月球上发射一颗绕它沿圆形轨道运行的卫星的最大周期为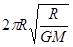

参考答案：B

本题解析：月球表面的重力加速根据黄金代换可知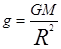：,物体上升的最大高度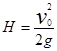=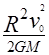,物体落回到抛出点所用时间,最大运行速度所以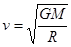。有最小周期没有最大周期。所以只有B对。

本题难度：一般

3、简答题  1789年英国著名物理学家卡文迪许首先估算出了地球的平均密度。根据你学过的知识，能否知道地球平均密度的大小。

参考答案：ρ＝5.5×103 kg/m3

本题解析：实际本题是要求进行估算，因而如何挖掘题目中的隐含条件是关键.而我们学过的知识中能与地球质量密度相联系的应首先想到万有引力定律，何况题设中提出了“卡文迪许”呢？
设地球质量为M，地球半径为R，地球表面的重力加速度为g，忽略地球自转的影响，根据万有引力定律得：
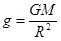?1
将地球看成均匀球体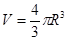：?2
由以上得地球的平均密度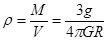
上式中π、G、R和g均为常数，将它们的值代入可得：
ρ＝5.5×103 kg/m3
即地球的平均密度为ρ＝5.5×103 kg/m3
[点评]?估算题中往往告诉的已知量很少或者什么量也不告诉，解题时就要求我们灵活地运用一些物理常数，如：重力加速度g、圆周率π、万有引力恒量G等等.

本题难度：简单

4、选择题  在地球表面上某点做竖直上抛实验，设地球为一密度均匀的球体，将小球以一定的速度竖直上抛，小球上升的最大高度为h、返回时间为t；若假设该点正下方某一深度处出现一较大的空腔，再以相同的速度重复实验，小球上升的最大高度为h′、返回时间为t′，则下列关系正确的是（　　）
A．h′＞h，t′＞t
B．h′＜h，t′＜t
C．h′＜h，t′＞t
D．h′＞h，t′＜t

参考答案：设地球的平均密度为ρ，地面和某深度空腔处的重力加速度分别为g1和g2，两处到地心的距离分别为r1和r2，在地表有G4πr31ρ3mr21=mg1，
则：g1=G4πr1ρ3，
在某深度空腔处有G=mg2，则g2=G4πr2ρ3，显然g1＞g2；小球做竖直上抛运动，由h=v22g和t=2vg，则h′＞h，t′＞t，故A正确．
故选A

本题解析：

本题难度：一般

5、选择题  我国将要发射一颗绕月运行的探月卫星“嫦娥1号”。设该卫星的轨道是圆形的且贴近月球表面、已知月球的质量约为地球质量的 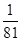，月球的半径约为地球半径的，地球上的第一宇宙速度约为7．9 km/s，则该探月卫星绕月运行的速率约为? (? )?
A．1.8 km/s
B．0.4 km/s
C．11 km/s
D．36 km/s

参考答案：A

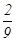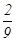本题解析：地球上第一宇宙速度为v1=，探月卫星所受万有引力等于向心力G＝m,解得v′=,因而＝，v1′=v1=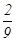×7.9km/s≈1.8km/s．

本题难度：一般