1、选择题  一宇宙飞船绕地球做匀速圆周运动，某时启动飞船的发动机点火加速，待它运动到距离地面的高度比原来高的位置，再定位使它又绕地球做匀速圆周运动，若不考虑飞船质量变化，则该飞船在后一轨道运行与在前一轨道运行相比
A．周期变长
B．动能变大
C．重力势能变大
D．机械能变大

参考答案：ACD

本题解析： 宇宙飞船绕地球做匀速圆周运动时满足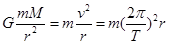：可得：
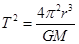?，,所以当飞船高度增加时，动能减小，周期变长，A正确，B错误；
由于高度增大，要克服万有引力做功，故重力势能增大，C正确；飞船从低轨道转移到高轨道，有个发动机点火加速过程，正是该过程增加了飞船的机械能，D正确。

本题难度：简单

2、填空题  一颗人造卫星在地球引力作用下，绕地球做匀速圆周运动，已知地球的质量为M，地球的半径为R，卫星的质量为m，卫星离地面的高度为h，引力常量为G，则地球对卫星的万有引力大小为______．

参考答案：根据万有引力定律表达式得：
F=GMmr2，其中r为物体到地球中心的距离，即r=R+h，
所以地球对卫星的万有引力大小为GMm(R+h)2．
故答案为：GMm(R+h)2．

本题解析：

本题难度：简单

3、填空题  （1）月球绕地球公转周期为T，月地距离为r，引力常量为G，地球质量为M，则r3与T2的比为k，k=______．
（2）一探月卫星在地月转移轨道上运行，计划通过地心和月心连线上特别位置，卫星在此处所受地球引力与月球引力的大小恰好相等．已知地球与月球的质量之比约为81：1，则该处到地心与到月心的距离之比约为______．

参考答案：（1）月球绕地球公转周期为T，月地距离为r，引力常量为G，地球质量为M，根据万有引力提供向心力，有：
GmMr2=mr(2πT)2
解得：
r3T2=GM4π2
故k=GM4π2
（2）卫星所受地球引力与月球引力的大小恰好相等，根据万有引力定律，有：
Gm0Mr21=Gm0mr22
解得：r2r1=

本题解析：

本题难度：简单

4、选择题  假想人类在进行探月活动中不断地向月球“移民”，经过较长时间后，月球和地球仍可视为均匀球体，地球的总质量仍大于月球的总质量，月球仍按原轨道运行，以下说法正确的是（　　）
A．月球绕地球运动的向心加速度将变大
B．月球绕地球运动的周期将变小
C．月球与地球之间的万有引力将变大
D．月球绕地球运动的线速度将变大

参考答案：A、根据GMmr2=ma=mv2r=mr4π2T2得，a=GMr2，v=

本题解析：

本题难度：简单

5、填空题  已知地球半径约为6.4×106 m，又知月球绕地球的运动可近似看作匀速圆周运动，则可估算出月球到地心的距离约为____________m．（结果只保留一位有效数字）

参考答案：4×108

本题解析：

本题难度：一般