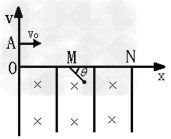
1、计算题  如图所示，直角坐标系xOy位于竖直平面内，在水平的x轴下方存在匀强磁场和匀强电场，磁场的磁感应为B，方向垂直xOy平面向里，电场线平行于y轴。一质量为m、电荷量为q的带正电的小球，从y轴上的A点水平向右抛出，经x轴上的M点进入电场和磁场，恰能做匀速圆周运动，从x轴上的N点第一次离开电场和磁场，MN之间的距离为L，小球过M点时的速度方向与x轴的方向夹角为θ。不计空气阻力，重力加速度为g，求
（1）电场强度E的大小和方向；
（2）小球从A点抛出时初速度v0的大小；
（3）A点到x轴的高度h。

参考答案：解：（1）小球在电场、磁场中恰能做匀速圆周运动，说明电场力和重力平衡（恒力不能充当圆周运动的向心力），有
?①
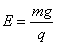?②
重力的方向竖直向下，电场力方向只能向上，由于小球带正电，所以电场强度方向竖直向上
（2）小球做匀速圆周运动，O′为圆心，MN为弦长，，如图所示。设半径为r，由几何关系知 ③
小球做匀速圆周运动的向心力由洛仑兹力提供，设小球做圆周运动的速率为v，有?④
由速度的合成与分解知 ⑤
由③④⑤式得 ⑥
（3）设小球到M点时的竖直分速度为vy，它与水平分速度的关系为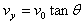 ⑦
由匀变速直线运动规律 ⑧
由⑥⑦⑧式得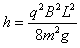 ⑨

本题解析：

本题难度：困难

2、计算题  如图所示，在xOy平面直角坐标系的第一象限有射线OA，OA与x轴正方向夹角为30°，OA与y轴所夹区域内有沿y轴负方向的匀强电场E1，第二象限存在水平向右的匀强电场E2，其它区域存在垂直于坐标平面向外的匀强磁场．有一质量为m、电荷量为q的带正电粒子，从y轴上的P点沿着x轴正方向以初速度v0射入电场，运动一段时间后经过Q点垂直于射线OA进入磁场，经磁场垂直x轴进入偏转电场E2，过y轴正半轴上的P点再次进入匀强电场E1，已知OP＝h，不计粒子重力，求：

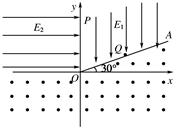
(1)粒子经过Q点时的速度大小；
(2)匀强电场电场强度E1的大小；
(3)粒子从Q点运动到P点所用的时间．

参考答案：(1)2v0　(2)　(3)＋

本题解析：(1)设粒子在Q的速度为v，则v·sin 30°＝v0?①
得v＝2v0.
(2)在电场E1中，对粒子有：h－OQsin 30°＝at2?③
OQ·cos 30°＝v0t?④
粒子的加速度：qE1＝ma?⑤
v·cos 30°＝at?⑥
得：E1＝
OQ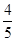＝h.
(3)粒子以O为圆心做匀速圆周运动
OQ＝r＝?⑦
T＝?⑧
在磁场中运动时间：t1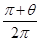＝·T＝?⑨
在电场E2中运动时间：t2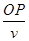＝＋?⑩
Q点运动到P点的时间：t＝t1＋t2＝＋.

本题难度：一般

3、选择题  如图所示，粗糙的平行金属导轨倾斜放置，导轨间距l=1m，导轨电阻不计，顶端QQ′之间连接一个阻值为R=1.5Ω的电阻和开关S，底端PP′处有一小段水平轨道相连，匀强磁场B垂直于导轨平面。断开开关S，将一根电阻不计质量为m=4kg的金属棒从AA′处由静止开始滑下，落在水平面上的FF′处；闭合开关S，将金属棒仍从AA′处由静止开始滑下，落在水平面上的EE′处；开关S仍闭合，金属棒从另一位置CC′处由静止开始滑下，仍落在水平面上的EE′处。（忽略金属棒经过PP′处的能量损失，金属棒始终与导轨垂直接触良好）测得相关数据为s=2m，h=5m，x1=2m，x2=1.5m，下列说法正确的是（?）

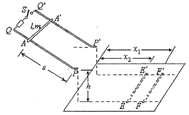
A．S断开时，金属棒沿斜面下滑的加速度为1m/s2
B．CC′一定在AA′的上方
C．B=2T
D．从AA＇处释放时，电阻R上产生的热量为3.5J

参考答案：ACD

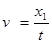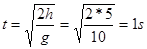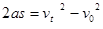本题解析：S断开，金属棒从静止开始滑下时，金属棒在斜面上作匀加速直线运动，在离开斜面以后，做平抛运动。金属棒在离开斜面时速度，，所以，由可得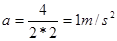，，A正确。S闭合，金属棒从滑下时，金属棒做变加速直线运动，加速度越来越小，在离开斜面以后，仍然做平抛运动。同理可得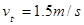，有能量守恒定理可得：电阻R上产生的热量，故D正确。开关S闭合后，金属棒从另一位置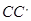由静止开始滑下，仍然落在，则说明金属棒在未离开斜面时，已做匀速直线运动，其速度为1.5m/s，所以?得，所以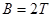.所以C正确。B不确定，也可以在下方。

本题难度：简单

4、计算题  （16分）如图甲所示，两水平放置的平行金属板A、B的板长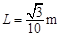，板间距离d=0.10m，在金属板右侧有一范围足够大，方向垂直于纸面向里的匀强磁场，磁感应强度B=1.0×10-2T，其左边界为y轴．在t=0时刻，两金属板间加如图乙所示的正弦交变电压．现从t=0开始，位于极板左侧的粒子源沿x轴向右以1000个/秒的数量连续均匀发射带正电的粒子，粒子均以的初速度沿x轴进入电场，经电场后部分粒子射入磁场．已知带电粒子的比荷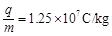，粒子通过电场区域的极短时间内，极板间的电压可以看作不变，不计粒子重力，不考虑极板边缘及粒子间相互影响．试求：

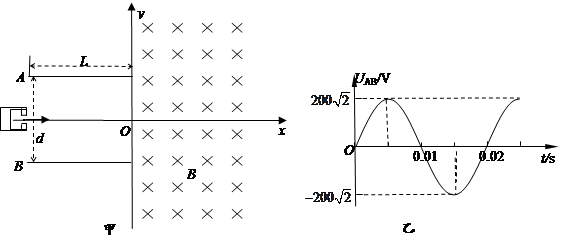
（1）t＝0时刻进入的粒子，经边界y轴射入磁场和射出磁场时两点间的距离；
（2）每秒钟有多少个粒子进入磁场；
（3）何时刻由粒子源进入的带电粒子在磁场中运动时间最长，求最长时间tm（π≈3）．

参考答案：（1）1.38m（2）每秒钟有500个粒子进入磁场（3）tm="3.2" ×10-5s

本题解析：（1）t＝0时，UAB=0，带电粒子在极板间不偏转，水平射入磁场，
由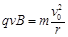：?(1分) 得：?(1分)
射入和射出磁场时，两点间的距离为?(1分)
（2）假设两极板电压为u时，由O点射入的粒子刚好从板的边缘进入磁场，则有
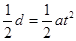?(1分) ；?(1分)；? (1分)；? (1分)；
解得：? (1分)
由乙图可知，在每个周期内，只有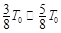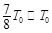，，时间段内由O射入的粒子才能通过电场进入磁场，即只有半个周期内有粒子能进入磁场，所以每秒钟有500个粒子进入磁场．（2分）
（3）只有当A板电势高于B板电势，且沿B板右侧边缘进入磁场的粒子，由于在电场中的偏转角最大，使得其在磁场中做圆周运动对应的圆心角最大，故在磁场中运动的时间最长，如图所示．即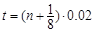：,（……）(1分)

或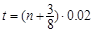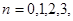：,（……）(1分)
这些时刻入射的粒子在磁场中运动的时间最长．
由带电粒子在电场中做类平抛运动的特点可得：?，θ=30°（1分）
设粒子在磁场中做匀速圆周运动的周期T，所求的最长?时间为tm，则有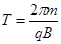：（1分）
由几何关系得粒子在磁场中运动的圆心角为，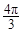
则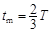：?（1分）?解得：tm="3.2" ×10-5s（1分
点评：本题难度较大，如果粒子以垂直磁场边界射入，必垂直磁场边界射出，处理带电粒子在匀强磁场中的偏转问题，首先要先画出大概的运动轨迹，先找圆心后求半径，处理边界磁场问题时，应巧妙应用对称性是解题的技巧

本题难度：一般

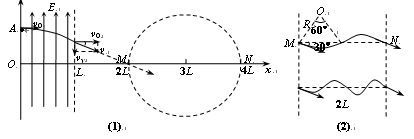
5、计算题   如图（甲）所示,在直角坐标系0≤x≤L区域内有沿y轴正方向的匀强电场,右侧有一个以点(3L,0)为圆心、半径为L的圆形区域,圆形区域与x轴的交点分别为M、N。现有一质量为m、带电量为e的电子,从y轴上的A点以速度v0沿x轴正方向射入电场,飞出电场后从M点进入圆形区域,速度方向与x轴夹角为30°。此时在圆形区域加如图（乙）所示周期性变化的磁场,以垂直于纸面向外为磁场正方向）,最后电子运动一段时间后从N点飞出,速度方向与进入磁场时的速度方向相同（与x轴夹角也为30°）。求:

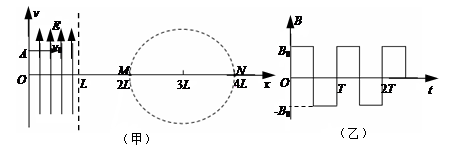
⑴ 电子进入圆形磁场区域时的速度大小；
⑵ 0≤x≤L区域内匀强电场场强E的大小；
⑶ 写出圆形磁场区域磁感应强度B0的大小、磁场变化周期T各应满足的表达式。

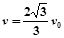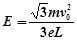参考答案：（1）（2）（3）

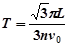
本题解析：本题考查带电粒子在复合场中的运动，难度较大，带电粒子先在匀强电场做类平抛运动，可以把出射速度分解后进行求解，出电场后带电粒子不受任何力的作用做匀速直线运动，可求出进入磁场时的速度方向，由磁场的可重复性可判断从N点射出时，带电粒子半径的表达式和周期表达式
⑴ 电子在电场中作类平抛运动,射出电场时,如图1所示.

由速度关系: ……2分?
解得?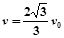…………2分
⑵ 由速度关系得…………2分
在竖直方向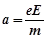…………1分?
…………1分
解得?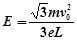…………2分
⑶在磁场变化的半个周期内粒子的偏转角为60°（如图2）,所以,在磁场变化的半个周期内,粒子在x轴方向上的位移恰好等于R。粒子到达N点而且速度符合要求的空间条件是: ?
…………2分?
电子在磁场作圆周运动，洛伦兹力提供向心力。
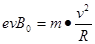………1分?
得?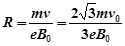……1分
解得， (n=1、2、3……) …………1分
若粒子在磁场变化的半个周期恰好转过1/6圆周,同时MN间运动时间是磁场变化周期的整数倍时,可使粒子到达N点并且速度满足题设要求。应满足的时间条件:
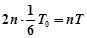…………1分?
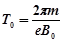…………1分
代入T的表达式得: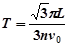(n=1、2、3……) …………1分

本题难度：一般