1、选择题  有一行星的密度跟地球密度相同，但它表面处的重力加速度是地面上重力加速度的4倍，则行星的质量是地球质量的（　　）
A．64倍
B．16倍
C．4倍
D．1/4倍

参考答案：根据万有引力等于重力，列出等式：GMmR2=mg
g=GMR2，其中M是地球的质量，R应该是物体在某位置到球心的距离．
根据根据密度与质量关系得：M=ρ?43πR3，星球的密度跟地球密度相同，
g1g2=R1R2=4
M1M2=R31R32=64
故选A．

本题解析：

本题难度：一般

2、选择题  若已知引力常量G=6. 67×10-11N ·m2/kg2 ，重力加速度g=9.8m/s2，地球半径R=6.4×106 m ，则可知地球质量的数量级是
[? ]
A．1018kg?
B．1020kg?
C．1022kg?
D．1024kg

参考答案：D

本题解析：

本题难度：简单

3、选择题  把火星和地球都视为质量均匀分布的球体．已知地球半径约为火星半径的2倍，地球质量约为火星质量的10倍．由这些数据可推算出（　　）
A．地球表面和火星表面的重力加速度之比为1：50
B．地球表面和火星表面的重力加速度之比为10：1
C．地球和火星的第一宇宙速度之比为

参考答案：A、B、地球半径约为火星半径的2倍，地球质量约为火星质量的10倍，根据公式g=GMR2，重力加速度之比为：g地g火=M地M火?(R火R地)2=101×(12)2=52，故A错误，B错误；
C、D、地球半径约为火星半径的2倍，地球质量约为火星质量的10倍，根据公式v=

本题解析：

本题难度：简单

4、选择题  要使两物体间万有引力减小到原来的

参考答案：根据万有引力定律的表达式：F=GMmR2
A、使两物体的质量各减少一半，距离保持不变，万有引力减小到原来的14，故A正确．
B、使两物体间距离变为原来的2倍，质量不变，万有引力减小到原来的14，故B正确．
C、使其中一个物体质量减为原来的14，距离不变，万有引力减小到原来的14，故C正确．
D、使两物体质量及它们之间的距离都减为原来的14，万有引力不变，故D错误．
故选ABC．

本题解析：

本题难度：简单

5、计算题  两个靠得很近的恒星称为双星，这两颗星必定以一定角速度绕二者连线上的某一点转动才不至于由于万有引力的作用而吸引在一起，已知两颗星的质量分别为M、m ，相距为L，试求：（1）两颗星转动中心的位置；（2）这两颗星转动的周期。

参考答案：R=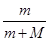L? T=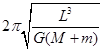

本题解析：

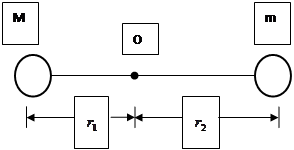
解：根据题意画出双星的运动图像如上图所示，双星间距为L，设两星球做匀速圆周运动的轨道半径分别为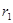、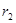，它们的转动周期T相同，
对m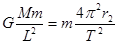：,①
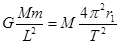对M：,②
由①②得，，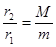
又因为，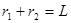
所以两颗星转动中心的位置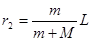,③
将③代入①可得,
这两颗星转动的周期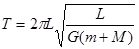

本题难度：简单