1、计算题  如图所示的正方形平面oabc内，存在着垂直于该平面向外的匀强磁场，磁感应强度大小为B，已知正方形边长为L，一质量为m，带电量为+q的粒子（不计重力）在t=0时刻平行于oc边从o点射入磁场中。
（1）若带电粒子从a点射出磁场，求带电粒子在磁场中运动的时间以及初速度的大小；
（2）若磁场的磁感应强度按如图所示的规律变化，规定磁场向外的方向为正方向，磁感应强度的大小为B0，则要使带电粒子能从oa边界射出磁场，磁感应强度B的变化周期T的最小值应为多少？
（3）若所加磁场与第（2）问中相同，则要使粒子从b点沿ab方向射出磁场，满足这一条件的磁感应强度的变化周期T及粒子射入磁场时的速度V0应为多少？（不考虑磁场变化产生的电场）

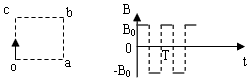
参考答案：解：（1）若带电粒子从a点射出磁场，则其做圆周运动的半径为r=L/2
所需时间为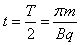
设粒子初速度的大小为v0，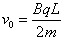
（2）若粒子从oa边射出，则其轨迹如图所示

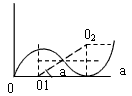
有，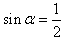
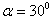
在磁场变化的半个周期内，粒子在磁场中旋转150°，其运动的时间为，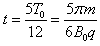
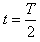
故磁场变化的最小周期为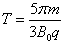
（3）要使粒子从b点沿ab方向射出磁场，其轨迹如图所示

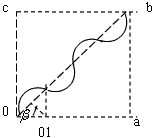
在磁场变化的半个周期中内，粒子在磁场中旋转的角度为2β，，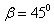
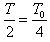
所以磁场变化的周期为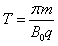
r=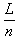（n=2，4，6 …. ），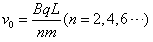

本题解析：

本题难度：困难

2、计算题  （18分）“太空粒子探测器”是由加速、偏转和收集三部分组成，其原理可简化如下：如图1所示，辐射状的加速电场区域边界为两个同心平行半圆弧面，圆心为O，外圆弧面AB的半径为L，电势为φ1，内圆弧面CD的半径为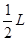，电势为φ2。足够长的收集板MN平行边界ACDB，O到MN板的距离OP=L。假设太空中漂浮着质量为m，电量为q的带正电粒子，它们能均匀地吸附到AB圆弧面上，并被加速电场从静止开始加速，不计粒子间的相互作用和其它星球对粒子引力的影响。

（1）求粒子到达O点时速度的大小；
（2）如图2所示，在边界ACDB和收集板MN之间加一个半圆形匀强磁场，圆心为O，半径为L，方向垂直纸面向内，则发现从AB圆弧面收集到的粒子经O点进入磁场后有2/3能打到MN板上（不考虑过边界ACDB的粒子再次返回），求所加磁感应强度的大小；
（3）同上问，从AB圆弧面收集到的粒子经O点进入磁场后均不能到达收集板MN，求磁感应强度所满足的条件。试写出定量反映收集板MN上的收集效率η与磁感应强度B的关系的相关式子。

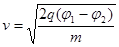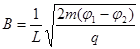参考答案：（1）；（2）；（3）。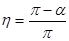

本题解析：（1）带电粒子在电场中加速时，由动能定理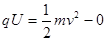，   （2分）
又U=φ1φ2        （2分）
所以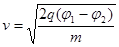：   （1分)
（2）从AB圆弧面收集到的粒子有2/3能打到MN板上，刚好不能打到MN上的粒子从磁场中出来后速度方向与MN平行，则入射的方向与AB之间的夹角是60°，在磁场中运动的轨迹如图1，轨迹圆心角θ=60°（2分）

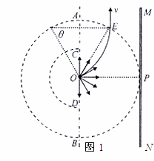
根据几何关系，粒子圆周运动的半径为r="L" （2分）
由牛顿第二定律得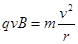： （1分）
联立解得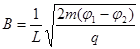：   （1分）
（3）当沿OD方向的粒子刚好打到MN上，则由几何关系可知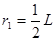，（2分）
由牛顿第二定律得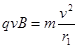： （1分）
得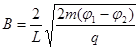：（1分），即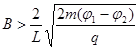（1分）
如图2，设粒子在磁场中运动圆弧对应的圆心角为α，由几何关系可知：

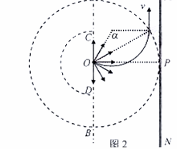
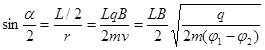 （1分）
MN上的收集效率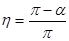：（1分
考点：动能定理，牛顿第二定律，带电粒子在磁场中的运动。

本题难度：困难

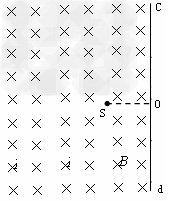
3、计算题  如图，真空室内存在一有右边界的匀强磁场区域，磁感应强度B=0.332T，磁场方向垂直于纸面向里，右边界cd为荧光屏（粒子打上去会发光）。在磁场中距荧光屏d=8cm处有一点状α粒子放射源S，可沿纸面向各个方向均匀放射初速率相同的α粒子，已知：α粒子的质量m=6.64×10－27 kg，电荷量q?=?3.2×10－19 C，初速?度v?=?3.2×106m/s。（可能用到的三角函数：sin37°=?0.6，sin30°=?0.5）求：
（1）α粒子在磁场中作圆周运动的轨道半径R；?
（2）荧光屏cd被α粒子射中而发光的区域长度L；
（3）若从放射源打出的α粒子总个数为3.6×1010个，则最终能打到荧光屏上的α粒子个数为多少？

参考答案：(1)R=20cm=0.2m
(2)o点上方16cm，o点下方16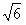cm，发光长度为：y=16（1+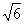）cm
(3)2.54×1010个

本题解析：

本题难度：一般

4、简答题  如图所示，有一对平行金属板，两板相距为0.05m．电压为10V；两板之间有匀强磁场，磁感应强度大小为B0=0.1T，方向与金属板面平行并垂直于纸面向里．图中右边有一半径R为0.1m、圆心为O的圆形区域内也存在匀强磁场，磁感应强度大小为B=

参考答案：（1）离子在平行金属板之间做匀速直线运动，洛仑兹力与电场力相等，即：
B0qv=qE0，
E0=Ud
解得：v=2000m/s
（2）在圆形磁场区域，离子做匀速圆周运动，由洛仑兹力公式和牛顿第二定律有：
Bqv=mv2r
由几何关系有：tanθ2=Rr
离子的比荷为：qm=2×104C/kg
（3）弧CF对应圆心角为θ，离子在圆形磁场区域中运动时间t，
t=θ2π?T
T=2πmqB
解得：t=θB0RdUtanθ2=

本题解析：

本题难度：一般

5、选择题  阿尔法磁谱仪（Alpha Magnetic Spectrometer）是一个安装于国际空间站上的微观粒子物理试验探究的设备。图为某简化了的磁谱仪部分构件的示意图，图中永磁铁提供匀强磁场，硅微条径迹探测器可以探测粒子在其中运动的轨迹。假设有a、b、c三种微观粒子从宇宙中垂直磁场方向飞入图中的匀强磁场（只考虑磁场对粒子的作用力），三粒子的质量与电量分别为a（m、＋q）、b（m、－q）、c(1800m、q)。则下列判断正确的有

A．a与b的偏转方向一定不同
B．a与b在磁场中运动轨迹的半径一定相同
C．仅依据粒子运动轨迹无法判断该粒子是b还是c
D．三粒子都不可能在该磁场中运动出完整的圆周轨迹