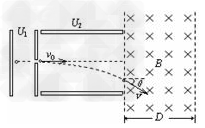
1、计算题  如图所示，一个质量为m =2.0×10-11 kg，电荷量q=+1.0×10-5 C的带电微粒（重力忽略不计），从静止开始经U1=100V电压加速后，水平进入两平行金属板间沿竖直方向的偏转电场中，偏转电场的电压U2=100V。金属板长L=20cm，两板间距d =cm。求：
（1）微粒进入偏转电场时的速度v0大小；
（2）微粒射出偏转电场时的偏转角θ；
（3）若该匀强磁场的宽度为D=cm，为使微粒不会由磁场右边射出，该匀强磁场的磁感应强度B至少多大。

2、选择题  如图所示，△ABC为与匀强磁场垂直的边长为a的等边三角形，磁场垂直纸面向外，比荷为e/m的电子以速度v0从A点沿AB方向射入磁场，现欲使电子能经过BC边，则磁感应强度B的取值应为（　　）
A．B＞

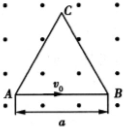
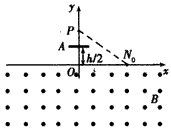
3、计算题  如图，在x轴下方有匀强磁场，磁感应强度大小为B，方向垂直于xy平面向外。P是y轴上距原点为h的一点，N0为x轴上距原点为a的一点。A是一块平行于x轴的挡板，与x轴的距离为h/2，A的中点在y轴上，长度略小于a/2。带电粒子与挡板碰撞前后，x方向的分速度不变，y方向的分速度反向、大小不变。质量为m，电荷量为q（q>0）的粒子从P点瞄准N0点入射，最后又通过P点，不计重力，求粒子入射速度的所有可能值。

4、计算题  如图，一束电子（电量为e）以速度v0垂直射入磁感应强度为B，宽为d的匀强磁场中，穿出磁场的速度方向与电子原来的入射方向的夹角为30°，求：
（1）电子的质量是多少？
（2）穿过磁场的时间是多少？
（3）若改变初速度，使电子刚好不能从A边射出，则此时速度v是多少？

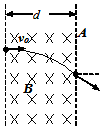
5、计算题  （18分）如图所示装置的左半部分为速度选择器，相距为d的两块平行金属板分别连在电压可调的电源两极上（上板接正极），板间存在方向垂直纸面向里、磁感应强度为B0的匀强磁场；右半部分为一半径为R的半圆形磁场区域，内有垂直纸面向外、磁感应强度为B的匀强磁场．矩形abcd相切于半圆，小孔M、N连线延长线经过圆心O点且与ad垂直．一束质量为m、带电量为+q的离子（不计重力）以不同速率沿MN方向从M孔射入．

（1）金属板间电压为U0时，求从N孔射出的离子的速度大小；
（2）要使离子能打到ab上，求金属板间电压U的取值范围．