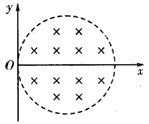
1、计算题 如图所示为圆形区域的匀强磁场,磁感应强度为B、方向垂直纸面向里,边界跟y轴相切于坐标原点O。O点处有一放射源,沿纸面向各方向射出速率均为v的某种带电粒子,带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍。已知该带电粒子的质量为m、电荷量为q,不考虑带电粒子的重力。
(1)推导带电粒子在磁场空间做圆周运动的轨道半径;
(2)求带电粒子通过磁场空间的最大偏转角;
(3)沿磁场边界放置绝缘弹性挡板,使粒子与挡板碰撞后以原速率弹回,且其电荷量保持不变。若从O点沿x轴正方向射入磁场的粒子速度已减小为v/2,求该粒子第一次回到O点经历的时间。
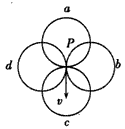
2、选择题 如图所示,带负电的粒子以速度v从粒子源P处射出,若图中匀强磁场范围足够大(方向垂直纸面),则带电粒子的可能轨迹是
[? ]
A.a
B.b
C.c
D.d
3、计算题 如图所示,质量为m,电荷量为e的电子从坐标原点O处沿xOy平面射入第一象限内,射入时的速度方向不同,但大小均为v0.现在某一区域内加一方向向外且垂直于xOy平面的匀强磁场,磁感应强度大小为B,若这些电子穿过磁场后都能垂直地射到与y轴平行的荧光屏MN上,求:

小题1:电子从y轴穿过的范围;
小题2:荧光屏上光斑的长度;
小题3:所加磁场范围的最小面积.
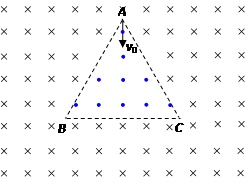
4、选择题 如图所示,边长为L的等边三角形ABC为两有界匀强磁场的理想边界,三角形内的磁场方向垂直纸面向外,磁感应强度大小为B,三角形外的磁场(足够大)方向垂直纸面向里,磁感应强度大小也为B。把粒子源放在顶点A处,它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v0的带电粒子(粒子重力不计)。若从A射出的粒子
①带负电, ,第一次到达C点所用时间为t1
,第一次到达C点所用时间为t1
②带负电, ,第一次到达C点所用时间为t2
,第一次到达C点所用时间为t2
③带正电, ,第一次到达C点所用时间为t3
,第一次到达C点所用时间为t3
④带正电, ,第一次到达C点所用时间为t4
,第一次到达C点所用时间为t4
则下列判断正确的是( )
A.t1= t3< t2= t4 B.t1< t2< t4 < t3
C.t1< t2< t3< t4 D.t1< t3< t2< t4
5、选择题 如图,有一矩形区域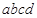 ,水平边
,水平边 长为s=
长为s=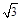 m,竖直边
m,竖直边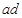 长为
长为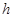 ="1" m。 质量均为
="1" m。 质量均为 、带电量分别为
、带电量分别为 和
和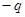 的两粒子,
的两粒子, 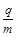 ="0.10" C/kg。当矩形区域只存在场强大小为E="10" N/C、方向竖直向下的匀强电场时,
="0.10" C/kg。当矩形区域只存在场强大小为E="10" N/C、方向竖直向下的匀强电场时, 由a点沿
由a点沿 方向以速率
方向以速率 进入矩形区域,轨迹如图。当矩形区域只存在匀强磁场时
进入矩形区域,轨迹如图。当矩形区域只存在匀强磁场时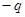 由c点沿cd方向以同样的速率
由c点沿cd方向以同样的速率 进入矩形区域,轨迹如图。不计重力,已知两粒子轨迹均恰好通过矩形区域的几何中心。则:
进入矩形区域,轨迹如图。不计重力,已知两粒子轨迹均恰好通过矩形区域的几何中心。则:
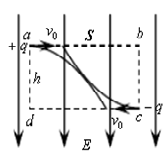
A.由题给数据,可求出初速度
B.磁场方向垂直纸面向外
C.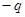 做匀速圆周运动的圆心在b点
做匀速圆周运动的圆心在b点
D.两粒子各自离开矩形区域时的动能相等。