1、填空题  如图所示，金属圆环半径为r，电阻的值为2R．金属杆oa一端可绕环的圆心O旋转，另一端a搁在环上，电阻值为R．另一金属杆ob一端固定在O点，另一端b固定在环上，电阻值也是R．加一个垂直圆环的磁感强度为B的匀强磁场，并使oa杆以角速度ω匀速旋转．如果所有触点接触良好，ob不影响oa的转动，流过oa的电流的最小值为______．

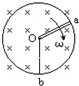
参考答案：oa杆切割磁感线产生感应电动势为：
E=Br.v=Br?12rω=12Br2ω，
当oa转到最高点时，外电路总电阻最大，通过oa的电流最小，最小电流为：
Imin=ER+R+0.5R=Br2ω5R；
故答案为：Br2ω5R．

本题解析：

本题难度：一般

2、简答题  如图，在水平台面上铺设了两根电阻不计的平行导轨MN和PQ，它们的宽度L=0.50m，水平部分是粗糙的，置于匀强磁场中，磁感应强度B=0.60T，方向竖直向上．倾斜部分较光滑，该处无磁场．直导线a和b可在导轨上滑动，质量均为m=0.20kg，电阻均为R=0.15．b放在导轨的水平部分，a置于斜轨高h=0.050m处无初速度释放(设在运动中a、b间距足够远且始终与导轨接触并垂直．回路感应电流的磁场不计，g=10m/s2)求:

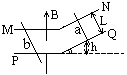
①由导线和导轨所组成回路的最大感应电流是多少?
②如果导线与水平导轨动摩擦因数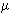=0.10，当导线b速度达到最大值
时，a的加速度大小是多少?

参考答案：（1）1A?（2）2m/s2

本题解析：

本题难度：一般

3、选择题  如图所示，一对大磁极，中间处可视为匀强磁场，上、下边缘处为非匀强磁场，一矩形导线框abcd保持水平，从两磁极间中心上方某处开始下落，并穿过磁场：

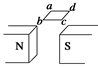
A．线框中有感应电流，方向是先a→b→c→d→a后d→c→b→a→d?
B．线框中有感应电流，方向是先d→c→b→a→d后a→b→c→d→a?
C．受磁场的作用，线框要发生转动
D．线框中始终没有感应电流

参考答案：D

本题解析：导线框从两极间中心上方某处开始下落，由于磁场的对称性，通过导线框的磁通量始终为零，所以线框中始终没有感应电流。
故选D
点评：注意产生感应电流的条件是：穿过闭合电路的磁通量发生变化。

本题难度：一般

4、计算题  如图所示，光滑的平行金属导轨CD与EF间距为L=1 m，与水平夹角为θ=30°，导轨上端用导线CE连接（导轨和连接线电阻不计），导轨处在磁感应强度为B=0.1 T、方向垂直于导轨平面向上的匀强磁场中。一根电阻为R=1 Ω的金属棒MN两端有导电小轮搁在两导轨上，棒上有吸水装置P。取沿导轨向下为x轴正方向，坐标原点在CE中点。开始时棒处在x=0位置（即与CE重合），棒的起始质量不计。当棒自静止起下滑时，便开始吸水，质量逐渐增大，设棒质量的增大与位移x的平方根成正比，即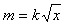，k为一常数，。
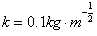(1)猜测金属棒下滑过程中做的是什么性质的运动，并加以证明；
(2)求金属棒下滑2m位移时速度为多大？

参考答案：解：(1)由于棒从静止开始运动，因此首先可以确定棒开始阶段做加速运动，如图所示，棒在下滑过程中沿导轨方向有向下的重力分力mgsinθ和向上的安培力F。由于m随位移x增大而增大，所以mgsinθ是一个变力；而安培力与速度有关，也随位移增大而增大。如果两个力的差值恒定，即合外力是恒力的话，棒有可能做匀加速运动，不妨假设棒做的是匀加速运动，且设下滑位移x时的加速度为ai

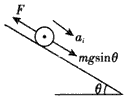
安培力
所以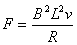
根据牛顿第二定律，有mgsinθ-F=mai
有
假设棒做匀加速运动，则瞬时速度
由于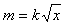，代入后得到
消去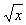后得到
从上述方程可以看出ai的解是一个定值，与位移x无关，这表明前面的假设成立，棒的运动确实是匀加速运动
(2)将题目给出的数据代入得到
化简有
令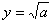，则上式可写作
解得y=2.17，即a=y2=4.71 m/s2
根据匀变速运动规律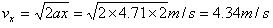

本题解析：

本题难度：困难

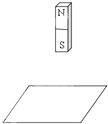
5、简答题  如图所示，桌面上放着一个单匝矩形线圈，线圈中心上方一定高度上有一竖直的条形磁铁，此时磁通量为0.04wb，把条形磁铁竖放在线圈内的桌面上时磁通量为0.12wb，分别计算以下两个过程中线圈中的感应电动势．
（1）用时0.5s
（2）换用10匝的线圈，用时0.1s．

参考答案：（1）根据法拉第电磁感应定律，有：
E=n△Φ△t=1×0.12-0.040.5=0.16V
（2）根据法拉第电磁感应定律，有：
E′=n△Φ△t=10×0.12-0.040.1=8V
答：（1）用时0.5s，线圈中的感应电动势为0.16V；
（2）换用10匝的线圈，用时0.1s，线圈中的感应电动势为8V．

本题解析：

本题难度：一般