1、计算题 【选修3-5选做题】
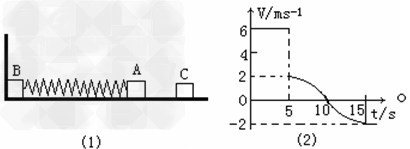
如图(1)所示,物体A、B的质量分别是4kg和8kg,由轻弹簧连接,静止放在光滑的水平面上,物体B左侧与竖直墙壁相接触。另有一个物体C水平向左运动,在t=5s时与物体A相碰,并立即与A有相同的速度,一起向左运动,物块C的速度-时间图象如图(2)所示。?
(1)求物块C的质量。
(2)弹簧压缩具有的最大弹性势能。?
(3)在5s到15s的时间内墙壁对物体B的作用力的冲量。
参考答案:解:(1)由图象可得:物体C以速度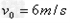 与A相碰,立即有相同的速度
与A相碰,立即有相同的速度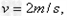 A、C相互作用时间很短,水平方向动量守恒,有:
A、C相互作用时间很短,水平方向动量守恒,有: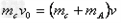
解得: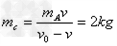
(2)物块C和A一起运动,压缩弹簧,它们的动能完全转化为弹性势能
最大弹性势能为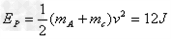
(3)5s到15s内,墙壁对B的作用力F等于轻弹簧的弹力,轻弹簧的弹力使物体A和C的速度由2m/s减到0,再反弹到2m/s,则弹力的冲量等于F的冲量为:
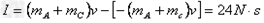 ,方向向右
,方向向右
本题解析:
本题难度:一般
2、简答题 如图所示,EF为水平地面,O点左侧是粗糙的、右侧是光滑的.一轻质弹簧右端与墙壁固定,左端与静止在O点质量为m的小物块A连结,弹簧处于原长状态.

质量为m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动,已知物块B与地面EO段间的滑动摩擦力大小为 ,物块B运动到O点与物块A相碰并一起向右运动(设碰撞时间极短),运动到D点时撤去外力F.已知CO=4s,OD=s.求撤去外力后:
,物块B运动到O点与物块A相碰并一起向右运动(设碰撞时间极短),运动到D点时撤去外力F.已知CO=4s,OD=s.求撤去外力后:
(1)弹簧的最大弹性势能;
(2)物块B最终离O点的距离.
参考答案:(1)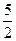 Fs?(2)5s
Fs?(2)5s
本题解析:(1)B与A碰撞前速度由动能定理
W=(F- F)·4s=
F)·4s=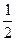 mv02
mv02
得v0= =
=
B与A碰撞,由动量守恒定律
mv0=2mv1
得v1=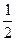

碰后到物块A、B运动至速度减为零,弹簧的最大弹性势能
Epm=F·s+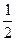 ·2mv12=
·2mv12=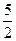 Fs.
Fs.
(2)设撤去F后,A、B一起回到O点时速度为v2,由机械能守恒得
Epm=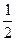 ·2mv22
·2mv22
v2=
返回至O点时,A、B开始分离,B在滑动摩擦力作用下向左做匀减速直线运动,设物块B最终离O点最大距离为x
由动能定理得:- Fx=0-
Fx=0-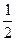 mv22
mv22
x=5s.
本题难度:一般
3、计算题 (15分)两个质量都是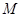 =0.4kg的砂箱A、B并排放在光滑的水平桌面上,一颗质量为
=0.4kg的砂箱A、B并排放在光滑的水平桌面上,一颗质量为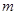 =0.1kg的子弹以
=0.1kg的子弹以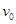 =140m/s的水平速度射向
=140m/s的水平速度射向 ,如图所示.射穿
,如图所示.射穿 后,进入
后,进入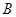 并同
并同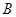 一起运动,测得
一起运动,测得 、
、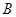 落点到桌边缘的水平距离
落点到桌边缘的水平距离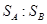 =1∶2,求:
=1∶2,求:
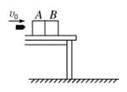
(1)沙箱 离开桌面的瞬时速度;(2)子弹在砂箱
离开桌面的瞬时速度;(2)子弹在砂箱 ?
?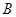 中穿行时系统一共产生的热量
中穿行时系统一共产生的热量 .
.
参考答案:(1)  ?(2)
?(2) 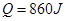
本题解析:(1)在子弹穿过A和B的过程中,A、B和子弹组成的系统满足动量守恒定律
设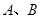 离开桌面的瞬时速度分别为
离开桌面的瞬时速度分别为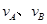 ,则
,则 ?①
?①
离开桌面后,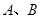 分别做平抛运动,则
分别做平抛运动,则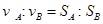 ?②
?②
联立①②解得 ,
,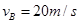
(2)子弹在砂箱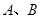 中穿行的过程,系统满足能量守恒则:
中穿行的过程,系统满足能量守恒则: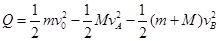 ?③
?③
解得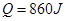
本题难度:困难
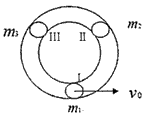
4、计算题 一水平放置的圆环形钢性窄槽固定在桌面上,槽内嵌着三个大小相同的钢性小球,它们的质量分别为m1、m2、m3,且m2=m3=2m1。小球与槽的两壁刚好接触且不计所有摩擦。起初三个小球处于如图所示的等间距的Ⅰ、Ⅱ、Ⅲ三个位置,m2、m3静止,m1以初速度v0=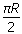 沿槽运动,R为圆环内半径与小球半径之和。已知m1以v0与静止的m2碰撞之后,m2的速度大小为2v0/3;m2与m3碰撞之后二者交换速度;m3与m1之间的碰撞为弹性碰撞。求此系统的运动周期T。
沿槽运动,R为圆环内半径与小球半径之和。已知m1以v0与静止的m2碰撞之后,m2的速度大小为2v0/3;m2与m3碰撞之后二者交换速度;m3与m1之间的碰撞为弹性碰撞。求此系统的运动周期T。
参考答案:解:设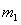 经过
经过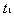 与
与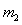 相碰,
相碰,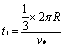 ?
?
设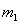 与
与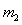 碰撞之后两球的速度分别为
碰撞之后两球的速度分别为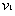 、
、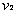 ,在碰撞过程中由动量守恒定律得:
,在碰撞过程中由动量守恒定律得:
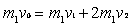 ?
?
因 ,求得
,求得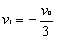 ,方向与碰前速度方向相反
,方向与碰前速度方向相反
设 经过
经过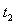 与
与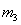 相碰,
相碰,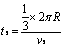 ?
?
设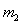 与
与 碰撞之后两球的速度分别为
碰撞之后两球的速度分别为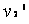 、
、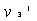 ,因
,因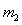 与
与 在碰撞后交换速度
在碰撞后交换速度
所以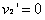 ,
,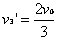
由碰后速度关系知, 与
与 碰撞的位置在Ⅰ位置,设
碰撞的位置在Ⅰ位置,设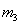 经过
经过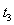 与
与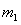 相碰,
相碰,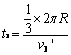 ?
?
设 与
与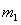 碰撞后的速度分别为
碰撞后的速度分别为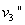 ,
,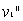 ,由动量守恒和机械能守恒定律可得:
,由动量守恒和机械能守恒定律可得:
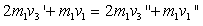 ?
?
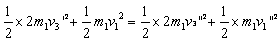 ?
?
联立得: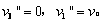 或
或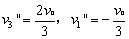 (舍)
(舍)
设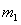 碰后经
碰后经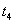 回到Ⅱ位置,
回到Ⅱ位置,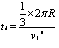 ?
?
至此,三个小球相对于原位置分别改变了120°,且速度与最初状态相同。故再经过两个相同的过程,即完成一个系统的运动周期
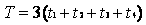
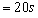
本题解析:
本题难度:困难
5、计算题 一速度为v的高速α粒子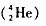 与同方向运动的氖核发生弹性正碰,碰后α粒子恰好静止求碰撞前后氖核
与同方向运动的氖核发生弹性正碰,碰后α粒子恰好静止求碰撞前后氖核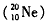 的速度(不计相对论修正)。
的速度(不计相对论修正)。
参考答案:解:设α粒子与氖核的质量分别为mα和mNe,氖核在碰撞前后的速度分别为vNe与vNe",
由动量守恒与机械能守恒定律,有 mαv十mNevNe=mNevNeˊ ①
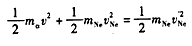 ②
②
解得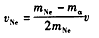 ③
③
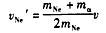 ④
④
已知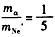 ⑤
⑤
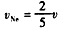 ⑥
⑥
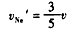 ⑦。
⑦。
本题解析:
本题难度:一般