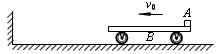
1、计算题 如图所示,一个物块A(可看成质点)放在足够长的平板小车B的右端,A、B一起以v0的水平初速度沿光滑水平面向左滑行。左边有一固定的竖直墙壁,小车B与墙壁相碰,碰撞时间极短,且碰撞前、后无能量损失。已知物块A与小车B的水平上表面间的动摩擦因数为μ,重力加速度为g。
(1)若A、B的质量比为k,且k=1,求物块A在小车B上发生相对运动的过程中物块A对小车的位移大小;
(2)若A、B的质量比为k,且k=2,为保证物块A在小车B上不掉下,求小车的最小长度;
(3)若A、B的质量比为k,求物块A在小车B上发生相对运动的时间。
参考答案:(1)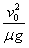
(2)
(3)当k<1时, ;当k>=1时,
;当k>=1时,
本题解析:
本题难度:困难
2、选择题 不定项选择
在两个物体碰撞前后,下列说法中可以成立的是( ? )
A.作用后的总机械能比作用前小,但总动量守恒
B.作用前后总动量均为零,但总动能守恒
C.作用前后总动能为零,而总动量不为零
D.作用前后总动量守恒,而系统内各物体的动量增量的总和不为零
参考答案:AB
本题解析:
本题难度:一般
3、计算题 太阳中含有大量的氘核,氘核不断发生核反应释放大量的核能,以光和热的形式向外辐射。已知氘核质量为2.0136 u,氦核质量为3.0150 u,中子质量为1.0087 u,1 u的质量相当于931.5 MeV的能量,则:
(1)完成核反应方程: 。
。
(2)求核反应中释放的核能。
(3)在两氘核以相等的动能0.35 MeV进行对心碰撞,并且核能全部转化为机械能的情况下,求反应中产生的中子和氦核的动能。
参考答案:解:(1)32He
(2)△E=△mc2=(2×2.0136 u-3.0150 u-1.0087 u)×931.5 MeV=3.26 MeV
(3)两核发生碰撞时:0=Mv1-mv2
由能量守恒可得:△E+2Ek=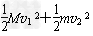
由以上两式解得:EHe=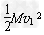 =0.99 MeV
=0.99 MeV
E中=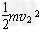 =2.97 MeV
=2.97 MeV
本题解析:
本题难度:一般
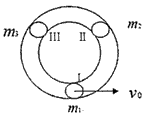
4、计算题 一水平放置的圆环形钢性窄槽固定在桌面上,槽内嵌着三个大小相同的钢性小球,它们的质量分别为m1、m2、m3,且m2=m3=2m1。小球与槽的两壁刚好接触且不计所有摩擦。起初三个小球处于如图所示的等间距的Ⅰ、Ⅱ、Ⅲ三个位置,m2、m3静止,m1以初速度v0=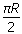 沿槽运动,R为圆环内半径与小球半径之和。已知m1以v0与静止的m2碰撞之后,m2的速度大小为2v0/3;m2与m3碰撞之后二者交换速度;m3与m1之间的碰撞为弹性碰撞。求此系统的运动周期T。
沿槽运动,R为圆环内半径与小球半径之和。已知m1以v0与静止的m2碰撞之后,m2的速度大小为2v0/3;m2与m3碰撞之后二者交换速度;m3与m1之间的碰撞为弹性碰撞。求此系统的运动周期T。
参考答案:解:设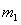 经过
经过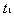 与
与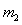 相碰,
相碰,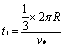 ?
?
设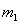 与
与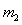 碰撞之后两球的速度分别为
碰撞之后两球的速度分别为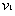 、
、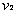 ,在碰撞过程中由动量守恒定律得:
,在碰撞过程中由动量守恒定律得:
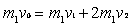 ?
?
因 ,求得
,求得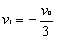 ,方向与碰前速度方向相反
,方向与碰前速度方向相反
设 经过
经过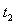 与
与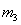 相碰,
相碰,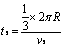 ?
?
设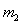 与
与 碰撞之后两球的速度分别为
碰撞之后两球的速度分别为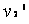 、
、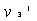 ,因
,因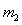 与
与 在碰撞后交换速度
在碰撞后交换速度
所以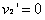 ,
,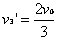
由碰后速度关系知, 与
与 碰撞的位置在Ⅰ位置,设
碰撞的位置在Ⅰ位置,设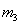 经过
经过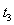 与
与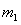 相碰,
相碰,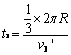 ?
?
设 与
与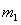 碰撞后的速度分别为
碰撞后的速度分别为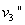 ,
,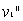 ,由动量守恒和机械能守恒定律可得:
,由动量守恒和机械能守恒定律可得:
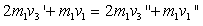 ?
?
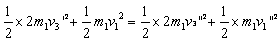 ?
?
联立得: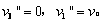 或
或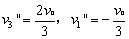 (舍)
(舍)
设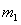 碰后经
碰后经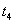 回到Ⅱ位置,
回到Ⅱ位置,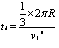 ?
?
至此,三个小球相对于原位置分别改变了120°,且速度与最初状态相同。故再经过两个相同的过程,即完成一个系统的运动周期
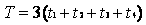
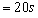
本题解析:
本题难度:困难
5、填空题 光滑水平面上有两个小球A和B,B的质量是A的2倍。小球A以速度v0向右运动,与静止的小球B发生对心碰撞,碰撞前后两球的运动都在一条直线上。若碰撞后B球的速度大小为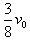 ,则碰撞后小球A的速度大小为___,小球A碰撞后的运动方向为___。
,则碰撞后小球A的速度大小为___,小球A碰撞后的运动方向为___。
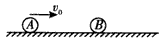
参考答案: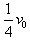 ,向右
,向右
本题解析:
本题难度:一般