1、选择题  质量相等的两个小球A、B，在光滑水平面上沿同一直线向同一方向运动.A球初动量为7 kg·m/s，B球的初动量为5 kg·m/s.当A追上B球发生碰撞后，A、B两球动量的可能值为（?）
A.pA="6" kg·m/s? pB="6" kg·m/s?B.pA="3" kg·m/s? pB="9" kg·m/s
C.pA="-2" kg·m/s? pB="14" kg·m/s?D.pA="-4" kg·m/s? pB="10" kg·m/s

参考答案：A

本题解析：该类题中发生的物理过程，应同时满足：碰撞前后系统动量守恒，即Δp=0，碰撞前后系统的动能不能增加，即ΔEk≤0.分析A、B、C、D四个选项，可知D不满足动量守恒，故D不正确.A、B、C三个选项均满足动量守恒，但B、C选项中，碰撞后系统的动能均大于碰撞前的系统动能，故B、C不正确，只有A正确.

本题难度：简单

2、计算题  如图，倾角为θ的斜面固定。有n个质量都为m的相同的小木块（可视为质点）放置在斜面上。相邻两小木块间距离都为l，最下端的木块距底端也是l，小木块与斜面间的动摩擦因数都为μ。在开始时刻，第一个小木块从斜面顶端以初速度v0沿斜面下滑，其余所有木块都静止，由于第一个木块的下滑将依次引起一系列的碰撞。设每次碰撞的时间极短，在每次碰撞后，发生碰撞的木块都粘在一起运动，直到最后第n个木块到达底端时，速度刚好为零。己知重力加速度为g。求：
（1）第一次碰撞后小木块l的速度大小v；
（2）从第一个小木块开始运动到第一次碰撞后系统损失的机械能△E；
（3）发生一系列碰撞后，直到最后第n个木块到达底端，在整个过程中，由于碰撞所损失的总机械能△E总。

参考答案：解：（1）设小木块1碰前的速度为v1，从开始运动到碰前，根据动能定理

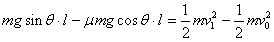
对小木块1和2，由动量守恒
求出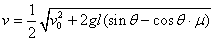
（2）碰撞前损失的机械能为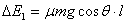
因碰撞损失的机械能为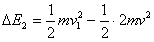
求出
（3）对n个木块碰撞的全过程
重力做的总功WG=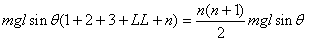
克服摩擦做的总功
根据功与能的关 系
由以上各式求出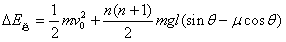

本题解析：

本题难度：困难

3、计算题  如果两球在碰撞前的速度在两球的中心连线上，那么这种碰撞称为对心碰撞（或称正碰），设两球碰撞前的速度分别为V10和V20，碰撞后的速度分别为V1和V2，并假定碰撞前后各个速度都沿同一方向，某探究学习小组从实验结果总结出一个碰撞定律：碰撞后两球的分离速度（V2－V1），与碰撞前两球的接近速度（V10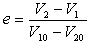－V20）成正比，比值由两球的材料性质决定，即通常把e叫做恢复系数。某同学利用如图所示装置进行实验，绳上挂有A、B两个小球，并已测出两球碰撞时的恢复系数e＝0.5，已知A球质量为2m、摆长为2L，B球质量为m、摆长为L，某次实验中球A由静止状态释放，运动到最低点与静止的球B发生正碰，碰后刚好使球B到达使绳成水平的位置。求球A释放前θ角的大小。

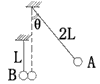
参考答案：解：设球A到达最底点的速度为V，根据机械能守恒有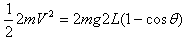 ①
所以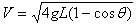
设碰撞后A、B两球的速率分别为VA、VB，由题意得：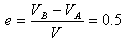
即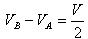 ②
A、B两球碰撞时水平方向动量守恒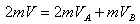： ③
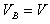由②③得 ④
碰撞后B球机械能守恒，故有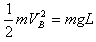： ⑤
将①④式代入⑤得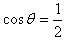
所以A球释放前θ＝60°

本题解析：

本题难度：困难

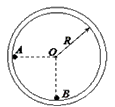
4、计算题  如图，半径为R的光滑圆形轨道固定在竖直面内。小球A、B质量分别为m、βm(β为待定系数)。A球从左边与圆心等高处由静止开始沿轨道下滑，与静止于轨道最低点的B球相撞，碰撞后A、B球能达到的最大高度均为，碰撞中无机械能损失。重力加速度为g。试求：
（1）待定系数β；
（2）第一次碰撞刚结束时小球A、B各自的速度和B球对轨道的压力；
（3）小球A、B在轨道最低处第二次碰撞刚结束时各自的速度，并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度。

参考答案：解：（1）由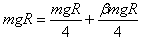，得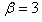
（2）设A、B碰撞后的速度分别为v1、v2，则

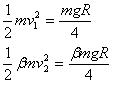
设向右为正、向左为负，解得
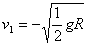，方向向左
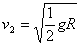，方向向右
设轨道对B球的支持力为N，B球对轨道的压力为N′，方向竖直向上为正、向下为负
则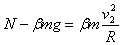
N′=-N=-4.5mg，方向竖直向下
（3）设A、B球第二次碰撞刚结束时的速度分别为V1、V2，则

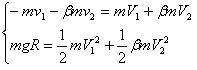
解得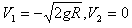（另一组解V1=-v1，V2=-v2不合题意，舍去）
由此可得：当n为奇数时，小球A、B在第n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同；
当n为偶数时，小球A、B在第n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同

本题解析：

本题难度：困难

5、计算题  如图所示，半径R=0.8m的四分之一光滑圆弧轨道位于竖直平面内，与长CD=2.0m的绝缘水平面平滑连接。水平面右侧空间存在互相垂直的匀强电场和匀强磁场，电场强度E=40N/C，方向竖直向上，磁场的磁感应强度B=1.0T，方向垂直纸面向外。两个质量均为m=2.0×10-6 kg的小球a和b，a球不带电，b球带q=1.0×10-6 C的正电，并静止于水平面右边缘处。将a球从圆弧轨道顶端由静止释放，运动到D点与b球发生正碰，碰撞时间极短，碰后两球粘合在一起飞入复合场中，最后落在地面上的P点。已知小球a在水平面上运动时所受的摩擦阻力f=0.1mg，PN=，取g=10m/s2。a、b均可作为质点。（结果保留三位有效数字）求：
（1）小球a与b相碰后瞬间速度的大小v；
（2）水平面离地面的高度h；
（3）从小球a开始释放到落地前瞬间的整个运过程中ab系统损失的机械能ΔE。

参考答案：解：（1）设a球到D点时的速度为vD，从释放至D点，根据动能定理：

对a、b球，根据动量守恒定律mvD=2mv
解得：v=1.73m/s
（2）两球进入复合场后，由计算可知Eq=2mg，两球在洛仑兹力作用下做匀速圆周运动轨迹示意图如图所示
?
洛仑兹力提供向心力
由图可知：r=2h　
解得：h=2=3.46m　
（3）ab系统损失的机械能
或
解得=1.49×10-4 J

本题解析：

本题难度：困难