1、计算题  如图，一半径为R的光滑绝缘半球面开口向下，固定在水平面上，整个空间存在匀强磁场，磁感应强度方向竖直向下，一电荷量为q(q＞0)，质量为m的小球P在球面上做水平的匀速圆周运动，圆心为O"，球心O到该圆周上任一点的连线与竖直方向的夹角为θ（0＜θ＜π/2）。为了使小球能够在该圆周上运动，求磁感应强度大小的最小值及小球P相应的速率，重力加速度为g。

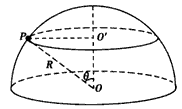
参考答案：解：据题意，小球P在球面上做水平的匀速圆周运动，该圆周的圆心为O"。P受到向下的重力mg、球面对它沿OP方向的支持力N和磁场的洛伦兹力f=qvB ①
式中v为小球运动的速率。洛伦兹力f的方向指向O"。根据牛顿第二定律有
Ncosθ-mg=0 ②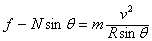， ③
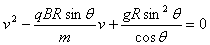由①②③式得?④
由于v是实数，必须满足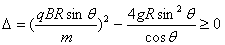?⑤
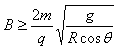由此得?⑥
可见，为了使小球能够在该圆周上运动，磁感应强度大小的最小值为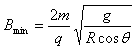 ⑦
此时，带电小球做匀速圆周运动的速率为 ⑧
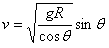由⑦⑧式得?⑨

本题解析：

本题难度：困难

2、选择题  空间有一圆柱形匀强磁场区域，该区域的横截面的半径为R，磁场方向垂直于横截面．一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场，离开磁场时速度方向偏离入射方向60°.不计重力，该磁场的磁感应强度大小为
A．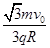
B．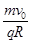
C．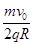
D．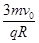

参考答案：A

本题解析：
　
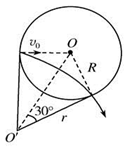
根据题意作出粒子运动的轨迹如图所示，由几何关系可得，粒子运动的半径r＝R，根据粒子受到的洛伦兹力提供向心力可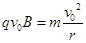得，，解得，，选项A正确．

本题难度：一般

3、填空题  摆线长为L，摆球质量为m带正电量q的单摆从如图所示位置A摆下，在一个磁感应强度为B的匀强磁场中运动，摆动平面垂直磁场，若图中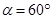，摆球从A开始运动，当它第一次到最低点时，摆线上的拉力大小为_____________．

参考答案：

本题解析：小球在下落过程中，只有重力做功，所以到最低点时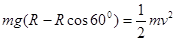，，小球在最低点时，根据左手定则可得受到竖直向下的洛伦兹力，故小球受到竖直向下的重力，竖直向上的拉力，竖直向下的洛伦兹力，它们的合力充当向心力，所以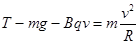
故两式联立可得

本题难度：简单

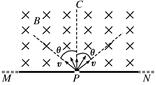
4、选择题  如图6所示，在屏MN的上方有磁感应强度为B的匀强磁场，磁场方向垂直于纸面向里．P为屏上的一个小孔．PC与MN垂直．一群质量为m、带电荷量为－q的粒子(不计重力)，以相同的速率v，从P处沿垂直于磁场的方向射入磁场区域．粒子入射方向在与磁场B垂直的平面内，且散开在与PC夹角为θ的范围内．则在屏MN上被粒子打中的区域的长度为? (　　) ?

A．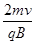
B．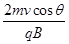
C．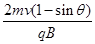
D．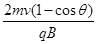

参考答案：D

本题解析：由图可知，沿PC方向射入磁场中的带负电的粒子打在MN上的点离P点最远，为PR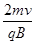＝，沿两边界线射入磁场中的带负电的粒子打在MN上的点离P点最近，为PQ＝cosθ，故在屏MN上被粒子打中的区域的长度为：QR＝PR－PQ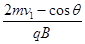＝，选项D正确．

本题难度：简单

5、选择题  如图所示，没有磁场时，显像管内电子束打在荧光屏正中的O点，加磁场后电子束打在荧光屏O点上方的P点，则所加磁场的方向可能是

[? ]
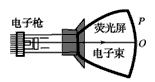
A．垂直于纸面向内　　　　　　
B．垂直于纸面向外
C．平行于纸面向上
D．平行于纸面向下

参考答案：B

本题解析：

本题难度：简单