1、计算题 (8分) 如图所示,质量为m的小球用长为L的轻质细线悬于O点,与O点处于同一水平线上的P点处有一根光滑的细钉,已知OP =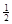 L,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则:
L,在A点给小球一个水平向左的初速度v0,发现小球恰能到达跟P点在同一竖直线上的最高点B,则:
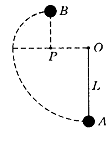
(1)小球到达B点时的速度多大?
(2)若不计空气阻力,则初速度v0多大?
(3)若初速度v0=3 ,则在小球从A到B的过程中克服空气阻力做了多少功?
,则在小球从A到B的过程中克服空气阻力做了多少功?
参考答案:(1) 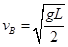 ?(2)
?(2) 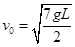 ?(3)
?(3) 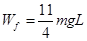
本题解析:(1)小球恰好到达最高点B,即在B点重力恰好提供向心力,所以有: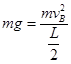 ,解得:
,解得: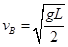
(2)从A到B,由动能定理知: ,解得:
,解得: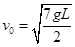
(3) 从A到B,由动能定理知: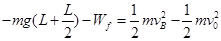 ,代入数据解得:
,代入数据解得: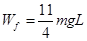
本题难度:一般
2、选择题 汽车拉着拖车在平直公路上匀速行驶.突然拖车与汽车脱钩,而汽车的牵引力不变,各自受的阻力不变.则脱钩后,在拖车停止运动前
①汽车和拖车的总动量不变 ?②汽车和拖车的总动能不变
③汽车和拖车的总动量增加 ?④汽车和拖车的总动能增加
以上说法正确的是( )
A.①
B.①④
C.②③
D.④
参考答案:①③分析汽车和拖车的受力可以知道,对于整体而言,牵引力和阻力的大小都没变,整体的合力还是为零,所以整体的动量守恒,所以①正确,③错误;
②④当拖车与汽车脱钩后,汽车的牵引力不变,但是车头受到的阻力减小,所以车头要做加速运动,拖车做减速运动,车头的位移大于拖车的位移,根据动能定理可知,此时牵引力的位移比阻力的位移大,牵引力的功比阻力的功大,所以汽车和拖车的总动能要增加,所以④正确,②错误.
故选B.
本题解析:
本题难度:简单
3、选择题 如图所示,质量为m的物体用细绳 穿过光滑小孔牵引在光滑水平面上做匀速圆周运动,拉力为某个值F时,转动半径为R,当拉力逐渐减小到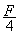 时,物体仍做匀速圆周运动,半径为2R,则外力对物体做功的大小是?
时,物体仍做匀速圆周运动,半径为2R,则外力对物体做功的大小是?
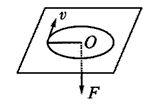
[? ]
A.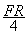
B.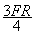
C.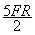
D.0
参考答案:
本题解析:
本题难度:简单
4、计算题 (18分)如图甲所示,粗糙水平面CD与光滑斜面DE平滑连接于D处;可视为质点的物块A、B紧靠一起静置于P点,某时刻A、B在足够大的内力作用下突然分离,此后A向左运动.
已知:斜面的高度H=1.2m;A、B质量分别为1kg和0.8kg,且它们与CD段的动摩擦因数相同;A向左运动的速度平方与位移大小关系如图乙;重力加速度g取10m/s2.

(1)求A、B与CD段的动摩擦因数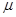 ;
;
(2)求A、B分离时B的速度大小vB;
(3)要使B能追上A,试讨论P、D两点间距x的取值范围.
参考答案:见解析
本题解析:解:(1)由图象可知,分离时物块A的初速度vA=4m/s,?①(1分)
A最终位置与P点距离sA=8m,?②(1分)
从A、B分离到A匀减速运动停止,有 ?③(1分)
?③(1分)
得A的加速度大小? a=1m/s2?④(1分)
由牛顿第二定律可知 ?⑤(2分)
?⑤(2分)
解得 ?μ=0.1?⑥(2分)
【或:从A、B分离到A匀减速运动停止,由动能定理
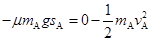 ?(3分)
?(3分)
解得 ?μ=0.1?(1分)】
(2)A、B分离过程,由动量守恒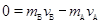 ?⑦(2分)
?⑦(2分)
解得 ?vB="5m/s" ?⑧(2分)
(3)(Ⅰ)若B恰好能返回并追上A, B从分离后到追上A过程由动能定理
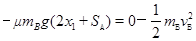 ?⑨?(2分)
?⑨?(2分)
解得? x1=2.25m?⑩?(1分)
(Ⅱ)若B恰好不冲出斜面,B从P到E过程由动能定理
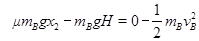 ?(2分)
?(2分)
解得 ?x2=0.50m?(1分)
综上,要使B能追上A,x应满足:2.25m≥L≥0.50m?
(评分说明:①~④各1分,⑤~⑧各2分,⑨?各2分,⑩?各1分)
本题难度:一般
5、选择题 如图中所示虚线表示等势面,相邻等势面间的电势差相等,有一带正电的小球在电场中运动,实线表示该小球的运动轨迹.小球在a点的动能等于20ev,b点的动能等于2ev.若取c点为零电势点,则当这个带电小球的电势能等于6eV时(不计重力和空气阻力),它的动能等于( )
A.16?ev
B.8?ev
C.6?ev
D.4?ev
