1、计算题  如图所示，质量为m＝0.1 kg可视为质点的小球从静止开始沿半径为R1＝35 cm的圆弧轨道AB由A点滑到B点后，进入与AB圆滑连接的1/4圆弧管道BC.管道出口处为C，圆弧管道半径为R2＝15 cm，在紧靠出口C处，有一水平放置且绕其水平轴线匀速旋转的圆筒(不计筒皮厚度)，筒上开有小孔D，筒旋转时，小孔D恰好能经过出口C处，若小球射出C出口时，恰好能接着穿过D孔，并且还能再从D孔向上穿出圆筒，小球到最高点后返回又先后两次向下穿过D孔而未发生碰撞，不计摩擦和空气阻力，g取10 m/s2，问：

(1)小球到达B点的瞬间前后对轨道的压力分别为多大？
(2)小球到达C点的速度多大？
(3)圆筒转动的最大周期T为多少？

参考答案：(1) N′1＝N1＝3 N；N′2＝N2＝5.7 N? (2) 0.2 s.?1分

本题解析：(1)AB过程机械能守恒：mgR1＝mvB2　vB＝m/s? 2分
到达B点瞬间前：N1－mg＝m? 1分
到达B点瞬间后：N2－mg＝m? 1分
依牛顿第三定律，对轨道的压力大小分别为N′1＝N1＝3 N；N′2＝N2＝5.7 N? 2
(2)小球向上穿过圆筒D孔又从D孔向上穿出所用的时间t1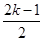＝T(k＝1、2、3……)；
小球向上穿出D孔后竖直上抛又返回到D孔进入圆筒所用时间为2t2＝nT(n＝1、2、3……)又由竖直上抛规律有：0＝vC－g(t1＋t2)? 1分
所以T＝? 2?分
当k＝n＝1时T有最大值，所以T＝0.2 s.? 1分
本题考查动能定理和圆周运动规律的应用，在B点为圆周运动的一部分，由支持力和重力的合力提供向心力，由动能定理可求得B点速度大小，再由向心力公式求得支持力大小，由A到C应用动能定理可求得C点速度大小，由于圆筒转动的周期性，经过半个周期的奇数倍时物体能从C点穿出，于是得到周期T的表达式，由此N=1时周期最大

本题难度：一般

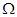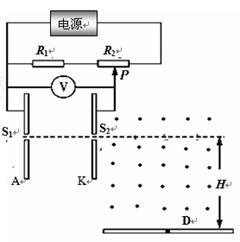
2、计算题  （18分）竖直平行放置的两个金属板A、K连在如图所示的电路中．电源电动势E=" 91" V，内阻r=1Ω，定值电阻R1=l0，滑动变阻器R2的最大阻值为80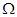, S1、S2为A、K板上的两个小孔，S1与S2的连线水平，在K板的右侧有一个水平方向的匀强磁场，磁感应强度大小为B="0." 10 T，方向垂直纸面向外．另有一水平放置的足够长的荧光屏D，如图H=0.2m．电量与质量之比为2.0×l05C/kg的带正电粒子由S1进入电场后，通过S2向磁场中心射去，通过磁场后打到荧光屏D上．粒子进入电场的初速度、重力均可忽略不计．
（1）两个金属板A、K各带什么电？
（2）如果粒子垂直打在荧光屏D上，求粒子在磁场中运动的时间和电压表的示数为多大？
（3）调节滑动变阻器滑片P的位置，当滑片到最左端时，通过计算确定粒子能否打到荧光屏？．

参考答案：（1）A极板带正电，（1分）K极板带负电（1分）（如果只答“A极板带正电”或“K极板带负电” ，给1分）?（2）7.9×10-5?s? 40V?（3）

本题解析：
（1）A极板带正电，（1分）K极板带负电（1分）
（如果只答“A极板带正电”或“K极板带负电” ，给1分）
（2）当粒子垂直打到D板上时，有粒子做圆周运动的半径 R=H?（1分）
设粒子的电荷量为q，质量为m，从S2穿出的速度为v0。
由牛顿运动定律得：??…………………………（2分）…
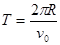?（1分）?=7.9×10-5?s?（1分）
两极板间的电压U即为电压表的读数，由动能定理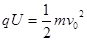：?（2分）
联立得 U= 40V（1分）
（3）由题知，当滑片到左端时，R2?有最小值，两极板间的电压最小。
由闭合电路欧姆定律，回路中的电流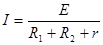：?=1A?（1分）
电阻R1两端电压? U1=IR1?（1分）?得U1=10V?（1分）
?（1分）
?（1分）
R1="0.1m" =" H" /2?（2分）
即恰好打在K板的正下方的D板上。（1分）

本题难度：一般

3、实验题  （6分）某同学利用图甲的实验装置做“探究动能定理”的实验。在尽量减小摩擦阻力的情况
下，先接通打点计时器的电源，再释放纸带，让质量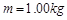的重物由静止下落，在纸带上打出一系列的
点，如图乙所示，A、B、C分别为所选取的计数点，且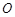为开始打出的第一点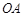，之间有若干点未标出，
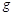相邻计数点的时间间隔为，重力加速度取。

（1）释放纸带前，纸带的____________（选填“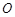”或“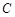”）端在上面；
（2）重物从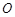运动到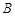的过程中，动能的变化量△（取两位有效数字）；
（3）列举一种能有效减小实验误差的做法_____________________________________.

参考答案：①C（2分）?②0.67 （2分）?③多次测量取平均值（2分）

本题解析：（1）因纸带打出的第一点是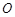点，故释放纸带前，纸带的C端在上面； （2）B带的速度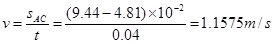,动能的变化量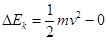=0.67J；（3）减小实验误差的做法是多次测量取平均值。

本题难度：一般

4、简答题  我国的“嫦娥奔月”月球探测工程已经启动，分“绕、落、回”三个发展阶段：在2007年已经发射了一颗围绕月球飞行的“嫦娥一号”卫星，将在2012年前后发射一颗月球软着陆器，在2017年前后发射一颗返回式月球软着陆器，进行首次月球样品自动取样并安全返回地球.设想着陆器完成了对月球表面的考察任务后，由月球表面回到围绕月球做圆周运动的轨道舱，如图19所示.为了安全，返回的着陆器与轨道舱对接时，必须具有相同的速度。设返回的着陆器质量为m，月球表面的重力加速度为g，月球的半径为R，月球的自转周期为T，轨道舱到月球中心的距离为r，已知着陆器从月球表面返回轨道舱的过程中需克服月球引力做功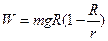，不计月球表面大气对着陆器的阻力和月球自转的影响，则
（1）着陆器与返回舱对接时的速度大小是多少？
（2）在月球表面的着陆器至少需要获得多少能量才能返回轨道舱？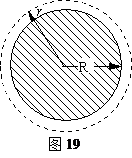

参考答案：（1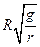）,（2）

本题解析：（1）着陆器在月球表面附近时：

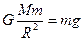
设轨道舱的质量为m0，运行速度大小为v，则：

联立可得：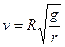
（2）着陆器与轨道舱对接时具有的动能为：?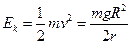
由动能定理得：

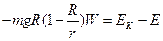
则着陆器返回时至少需要能量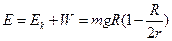

本题难度：简单

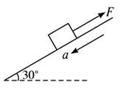
5、选择题  如图所示，具有初速度的物块，沿倾角为30°、粗糙的斜面向上运动的过程中，受一个恒定的沿斜面向上的拉力F作用，这时物块?加速度的大小为4m/s2，方向沿斜面向下.那么在物块向上运动过程中，正确的说法是

A．物块的机械能一定增加
B．物块的机械能一定减少
C．物块的机械能有可能不变
D．物块的机械能可能增加也可能减少

参考答案：A

本题解析：
试题分析: 设物块的质量为m，拉力与摩擦力的合力大小为F′，根据牛顿第二定律得知，物体所受的合力大小为4m，方向没斜面向下，而重力沿斜面的分力mgsin30°=5m，所以F′沿斜面向上，大小为m，物块沿斜面向上运动，拉力与摩擦力的合力F′做正功，物体的机械能增加，故A正确，BCD错误．

本题难度：一般