1、计算题 在 光滑水
光滑水 平面上,甲、乙两物体的质量分别为m1、m2,它们沿一条直线相向运动,其中甲物体运动速度v1的大
平面上,甲、乙两物体的质量分别为m1、m2,它们沿一条直线相向运动,其中甲物体运动速度v1的大 小是6 m/s,乙物体运动速度v2的大小是2 m/s。已知两物体碰撞后各自沿着原方向的反方向运动,速度v的大小都是4 m/s,求甲、乙两物体的质量之比。
小是6 m/s,乙物体运动速度v2的大小是2 m/s。已知两物体碰撞后各自沿着原方向的反方向运动,速度v的大小都是4 m/s,求甲、乙两物体的质量之比。
参考答案:解:设甲的初速度v1方向为正方向,则根据动量守恒定律有
m1v1-m2v2=-m1v+m2v
代入数据解得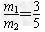
本题解析:
本题难度:一般
2、计算题 如图所示,在光滑水平面上有一质量为M的长木板,长木板上有一质量为m的小物块,它与长木板间的动摩擦因数为μ。开始时,长木板与小物块均靠在与水平面垂直的固定挡板处,某时刻它们以共同的速度v0向右运动,当长木板与右边的固定竖直挡板碰撞后,其速度的大小不变、方向相反,以后每次的碰撞均如此。设左右挡板之间的距离足够长,且M>m。
(1)要想物块不从长木板上落下,则长木板的长度L应满足什么条件?
(2)若上述条件满足,且M=2 kg,m=1 kg,v0=10 m/s,求整个系统在第5次碰撞前损失的所有机械能。
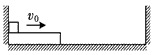
参考答案:解:(1)设第1次碰撞后小物块与长木板共同运动的速度为v1,第n次碰撞后小物块与长木板共同运动的速度为vn。每次碰撞后,由于两挡板的距离足够长,物块与长木板都能达到相对静止,第1次若不能掉下,往后每次相对滑动的距离会越来越小,更不可能掉下。由动量守恒定律和能量守恒定律有:
(M-m)v0=(M+m)v1
μmgs=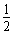 (m+M)v02-
(m+M)v02-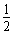 (M+m)v12
(M+m)v12
解得:s=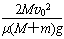
故L应满足的条件是:L≥s=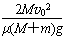
(2)第2次碰撞前有:(M-m)v0=(M+m)v1
第3次碰撞前有:(M-m)v1=(M+m)v2
第n次碰撞前有:(M-m)vn-2=(M+m)vn-1
所以vn-1=(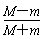 )n-1v0
)n-1v0
故第5次碰撞前有:v4=(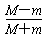 )4v0
)4v0
故第5次碰撞前损失的总机械能为:ΔE=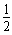 (M+m)v02-
(M+m)v02-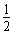 (M+m)v42
(M+m)v42
代入数据解得:ΔE=149.98 J
本题解析:
本题难度:困难
3、选择题 水平面上,一白球与一静止的灰球碰撞,两球质量相等。碰撞过程的频闪照片如图所示,据此可推断,碰撞过程中系统损失的动能约占碰撞前动能的

A.30%
B.50%
C.70%
D.90%
参考答案:A
本题解析:闪光照片的闪光时间是相等的,根据图上照片的间距可推知白球和灰球在碰撞前后的速度的关系,再根据动能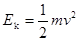 可推知碰后白球和灰球与碰撞前的白球的动能关系,进而可推知系统碰撞中损失的动能。
可推知碰后白球和灰球与碰撞前的白球的动能关系,进而可推知系统碰撞中损失的动能。
通过直尺可测量出碰前的白球照片间距与碰后白球照片间距及灰球照片间距的比值约为1.5∶0.9∶0.9,设碰撞前白球的速度为v0,碰撞后白球速度大小为v1,灰球速度大小为v2,由于闪光时间是相等的,则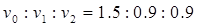 ,根据系统损失的动能
,根据系统损失的动能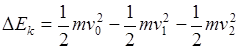 可解得
可解得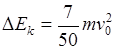 ,则
,则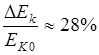 ,与选项A接近,故本题答案为A。
,与选项A接近,故本题答案为A。
【考点定位】本题考查动能、速度、位移与频闪照相相结合。通过对频闪照片的观察与测量,估测出碰撞前后小球的速度关系,进而推知动能的关系,有效考查考生的观察能力与分析能力。较难。
本解析为名师解析团队原创,授权独家使用,如有盗用,依法追责!
本题难度:一般
4、计算题 如果α粒子以速度v与电子发生弹性正碰(假定电子原来是静止的),求碰撞后仅粒子的速度变化了多少?并由此说明:为什么原子中的电子不能使α粒子发生明显的偏转?
参考答案:解:设α粒子初速度为v,质量为M,与电子碰后速度为v1,电子质量为m,与α粒子碰后速度为v2
由动量守恒定律得Mv=Mv1+mv2 ①
由能量关系得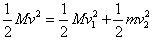 ?②
?②
由①②得碰后α粒子速度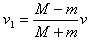 ③
③
α粒子速度变化量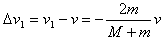 ④
④
把M=7 300m代入④得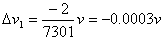
可见α粒子的速度变化只有万分之三,说明原子中的电子不能使α粒子发生明显的偏转
本题解析:
本题难度:一般
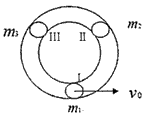
5、计算题 一水平放置的圆环形钢性窄槽固定在桌面上,槽内嵌着三个大小相同的钢性小球,它们的质量分别为m1、m2、m3,且m2=m3=2m1。小球与槽的两壁刚好接触且不计所有摩擦。起初三个小球处于如图所示的等间距的Ⅰ、Ⅱ、Ⅲ三个位置,m2、m3静止,m1以初速度v0=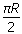 沿槽运动,R为圆环内半径与小球半径之和。已知m1以v0与静止的m2碰撞之后,m2的速度大小为2v0/3;m2与m3碰撞之后二者交换速度;m3与m1之间的碰撞为弹性碰撞。求此系统的运动周期T。
沿槽运动,R为圆环内半径与小球半径之和。已知m1以v0与静止的m2碰撞之后,m2的速度大小为2v0/3;m2与m3碰撞之后二者交换速度;m3与m1之间的碰撞为弹性碰撞。求此系统的运动周期T。
参考答案:解:设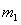 经过
经过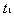 与
与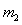 相碰,
相碰,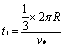 ?
?
设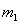 与
与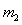 碰撞之后两球的速度分别为
碰撞之后两球的速度分别为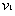 、
、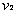 ,在碰撞过程中由动量守恒定律得:
,在碰撞过程中由动量守恒定律得:
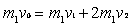 ?
?
因 ,求得
,求得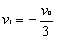 ,方向与碰前速度方向相反
,方向与碰前速度方向相反
设 经过
经过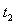 与
与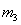 相碰,
相碰,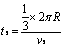 ?
?
设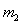 与
与 碰撞之后两球的速度分别为
碰撞之后两球的速度分别为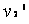 、
、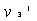 ,因
,因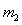 与
与 在碰撞后交换速度
在碰撞后交换速度
所以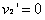 ,
,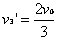
由碰后速度关系知, 与
与 碰撞的位置在Ⅰ位置,设
碰撞的位置在Ⅰ位置,设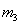 经过
经过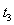 与
与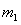 相碰,
相碰,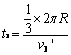 ?
?
设 与
与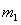 碰撞后的速度分别为
碰撞后的速度分别为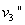 ,
,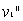 ,由动量守恒和机械能守恒定律可得:
,由动量守恒和机械能守恒定律可得:
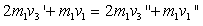 ?
?
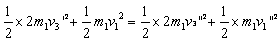 ?
?
联立得: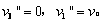 或
或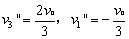 (舍)
(舍)
设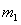 碰后经
碰后经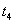 回到Ⅱ位置,
回到Ⅱ位置,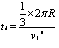 ?
?
至此,三个小球相对于原位置分别改变了120°,且速度与最初状态相同。故再经过两个相同的过程,即完成一个系统的运动周期
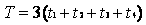
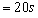
本题解析:
本题难度:困难