1、计算题  （14分）如图所示，AB是一段位于竖直平面内的光滑轨道，高度为h，末端B处的切线方向水平．一个质量为m的小物体P从轨道顶端A处由静止释放，滑到B端后飞出，落到地面上的C点，轨迹如图中虚线BC所示．已知它落地时相对于B点的水平位移OC＝l．现在轨道下方紧贴B点安装一水平传送带，传送带的右端与B的距离为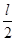．当传送带静止时，让P再次从A点由静止释放，它离开轨道并在传送带上滑行后从右端水平飞出，仍然落在地面的C点．（不计空气阻力）

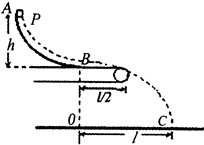
（1）求P滑至B点时的速度大小；
（2）求P与传送带之间的动摩擦因数μ；
（3）当传送带运动时（其他条件不变），P的落地点为仍为C点，求传送带运动方向及速度v的取值范围．

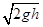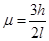参考答案：（1）；（2）；（3）方式一：当传送带向右运动时，若传送带的速度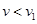，即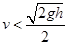时，物体在传送带上一直做匀减速直线运动，离开传送带的速度仍为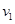，P的落地点仍为C点。?（2分）
方式二：当传送带向左运动时，速度无大小要求，物体都一直做匀减速运动，离开传送带的速度仍为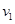，P的落地点仍为C点；?（2分）

本题解析：（1）物体P在AB轨道上滑动时，根据动能定理有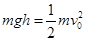?（2分）
P滑到B点时的速度为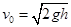?（1分）
（2）当没有传送带时，物体离开B点后做平抛运动，运动时间为t， 则有：
?（1分）
当B点下方的传送带静止时，物体从传送带右端水平抛出，在空中运动的时间也为t，水平位移为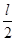，因此物体从传送带右端抛出的速度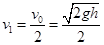：?（2分）
由牛顿第二定律得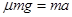：?（1分）
由运动学公式得：?（2分）
解得物体与传送带之间的动摩擦因数为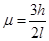：?（1分）
（3）方式一：当传送带向右运动时，若传送带的速度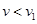，即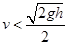时，物体在传送带上一直做匀减速直线运动，离开传送带的速度仍为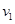，P的落地点仍为C点。?（2分）
方式二：当传送带向左运动时，速度无大小要求，物体都一直做匀减速运动，离开传送带的速度仍为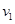，P的落地点仍为C点；?（2分）

本题难度：一般

2、选择题  如图所示，一钢球系在弹性绳的一端．绳的另一端固定在天花板上．先把钢球托起，然后由静止释放．若弹性绳的伸长始终在弹性限度内，关于钢球的加速度a与速度v分别随时间t变化的图象，下列说法正确的是（　　）

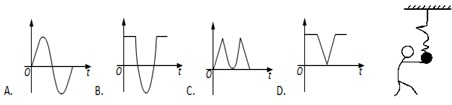
A．图B表示a-t图象，图A表示v-t图象
B．图B表示a-t图象，图C表示v-t图象
C．图D表示a-t图象，图C表示v-t图象
D．图D表示a-t图象，图A表示v-t图象

参考答案：将小球自由下落过程：小球仅受重力，故小球的加速度a=g，故a-t图象是一条水平的直线．小球的速度v=gt，由于速度图象的斜率等于物体的加速度，故v-t图象是过坐标原点的一条直线．
绳子张紧后：绳子的弹力F=kx，其中x为绳子的形变量，故小球的加速度a=mg-kxm=g-kxm，故随x的增大，物体的加速度a逐渐减小．但速度逐渐增大；故v-t图象的斜率逐渐减小．
当弹力等于重力时物体的加速度a=0，速度达到最大．此后弹力大于重力，故小球所受合力方向竖直向上．加速度a=kxm-g，随x增大物体的加速度逐渐增大，方向竖直向上．由于速度方向向下，故物体做加速度逐渐增大的变减速运动．
当物体的速度为0后物体开始向上做加速度逐渐减小的变加速运动，此过程中速度方向向上，加速度方向也向上．当弹力等于重力后物体做加速度逐渐增大的变减速运动，它的速度方向向上，加速度方向方向向下．当弹性绳恢复原长后速度向上，加速度a=g，即物体做竖直上抛运动．故图B表示a-t图象．
图A表示v-t图象．故A正确．
故选A．

本题解析：

本题难度：一般

3、计算题  如图所示，一小物体（可看做质点）从A点以v0=4m/s的初速度滑上斜面，上滑到B点后沿原路返回。A到B的距离为1m，斜面的倾角θ=37°。（g取10m/s2）

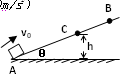
小题1:求小物体与斜面间的动摩擦因数μ
小题2:取水平地面为零重力势能面，若小物体返回经过C点时其动能恰好与重力势能相等，则C点相对水平地面的高度h为多大？

参考答案：
小题1:
小题2: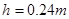

本题解析：①（7分）设物体的质量为m，物体与斜面间的动摩擦因数为μ。物体有A上滑到B做匀减速运动，设加速度的大小为a，由牛顿第二定律得：
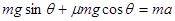?（2分）
又由运动学公式可得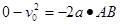：（2分）
代入数据可解得：?（2分）
②（7分）设物体返回经过C点时速度的大小为v1，对于物体从B到C的过程，由动能定理有：?（3分）
又根据题意有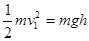：?（3分）
代入数据可得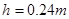：?（2分）

本题难度：简单

4、选择题  如图所示为甲、乙两质点的速度-时间图象，下列说法中正确的是（　　）

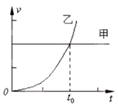
A．甲做直线运动，乙做曲线运动
B．甲做的是匀速运动，乙做的是加速度增大的加速运动
C．在0到t0时间内甲的位移等于乙的位移
D．在t0时刻甲、乙相遇，相遇前甲的速度大于乙的速度

参考答案：A、甲乙两质点的速度-时间图象都在t轴上方，速度均为正值，都沿正方向，两个质点都做直线运动．故A错误．
B、甲的速度不随时间变化，做匀速直线运动．乙的速度增大，图线切线的斜率逐渐增大，加速度增大，所以乙做加速度增大的加速运动，故B正确．
C、根据“面积”大小表示位移，可知在0～t0内，甲的位移大于乙的位移．故C错误．
D、在t0时刻甲乙的速度相同，由于起点位置关系不清楚，无法判断两车是否相遇．故D错误．
故选：B

本题解析：

本题难度：一般

5、计算题  （12分）一水平传送带以2.0m／s的速度顺时针传动，水平部分长为2.0m。，其右端与一倾角为θ=37°的光滑斜面平滑相连，斜面长为0.4m，一个可视为质点的物块无初速度地放在传送带最左端，已知物块与传送带间动摩擦因数μ=0.2，试问：

(1)物块能否到达斜面顶端?若能则说明理由，若不能则求出物块沿斜面上升的最大距离．
(2)物块从出发到4.5s末通过的路程．(sin37°=0.6， g取l0 m/s2)

参考答案：（1）s2<0.4m? (2) s=5m

本题解析：（1）物块在传送带上先做匀加速直线运动
μmg=m?al?①?（1分）
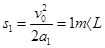?②（1分）
所以在到达传送带右端前物块已匀速
物块以ν0速度滑上斜面
一mgsinθ=ma2?③（1分）
物块速度为零时上升的距离
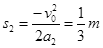?④?（1分）
由于s2<0.4m，所以物块未到达斜面的最高点．?（1分）
(2)（7分）物块从开始到第一次到达传送带右端所用时间
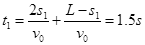?⑥?（1分）
物块在斜面上往返一次时间
?⑦?（1分）
物块再次滑到传送带上速度仍为ν0，方向向左
一μmg =ma3?⑧?（1分）
向左端发生的最大位移
?⑨(2分)
物块向左的减速度和向右的加速过程中位移大小相等
4.5s末物块在斜面上速度恰好减为零
故物块通过的总路程
s=L+3s2+2s3?⑩? (2分)
s=5m

本题难度：一般