1、简答题  （1）历史中在利用加速器实现的核反应，是用加速后动能为0.5MeV的质子11H轰击静止的X，生成两个动能均为8.9MeV的24He．（1MeV=1.6×-13J）
①上述核反应方程为______．
②质量亏损为______kg．
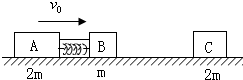
（2）如图所示，光滑水平面轨道上有三个木块，A、B、C，质量分别为mB=mc=2m，mA=m，A、B用细绳连接，中间有一压缩的弹簧（弹簧与滑块不栓接）．开始时A、B以共同速度v0运动，C静止．某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三滑块速度恰好相同．求B与C碰撞前B的速度．

参考答案：
（1）11H+37X→24He+24He或11H+37Li→24He+24He，
由质能方程得：△m=EC2=3.1×10-29Kg．
（2）设共同速度为v，球A和B分开后，B的速度为vB
由动量守恒定律有（mA+mB）v0=mAv+mBvB…①
mBvB=（mB+mC）…②
联立这两式得B和C碰撞前B的速度为vB=95v0．

本题解析：

本题难度：一般

2、简答题  在水平光滑细杆上穿着A、B两个刚性小球（可看作质点），用两根长度同为L的不可伸长的轻绳与C球连接，如图所示．已知A、B、C三球质量均相同，开始时三球均静止、两绳伸直且处于水平状态．现同时释放三球，求：
（l）在C球运动到最低点．A、B两球刚要相碰的瞬间，A、B两球速度的大小；
（2）在A、B相碰前的某一时刻，A、B二球速度v的大小与C球到细杆的距离h之间的关系．

参考答案：

（1）C到达最低点时速度为零，设A、B、C的质量均为m，
A、C组成的系统在水平方向动量守恒，
由动量守恒定律得：mvA+mvB=0，
A、B、C组成的系统机械能守恒，
由机械能守恒定律可得：mgL=12mvA2+12mvB2，
解得：vA=

本题解析：

本题难度：一般

3、简答题  在实验室里为了验证动量守恒定律，一般采用如图所示装置：
（1）为了保证小球做平抛运动，必须调整斜槽使______．
（2）若入射小球质量为m1，半径为r1；被碰小球质量为m2，
半径为r2，则?m1______m2，r1______r2?（填“＞”，“＜”或“=”）
（3）入射球每次从______滚下；
（4）碰撞过程中动量守恒，则由图可以判断出P是______小球落地点，M是______小球的落地点．
（5）找小球落地点时，一定要重复多次，找出小球落地点的平均位置，其方法是_______．
（6）用题中的字母写出体现动量守恒定律的表达式：______．

参考答案：（1）为了保证小球做平抛运动，即小球离开槽口时的速度的方向沿水平方向，必须调整斜槽使其末端切线水平；
（2）在小球碰撞过程中水平方向动量守恒定律故有m1v0=m1v1+m2v2
在碰撞过程中动能守恒故有12m1v20=12m1v21+12m2v22
解得v1=m1-m2m1+m2v0
要碰后入射小球的速度v1＞0，即m1-m2＞0，
m1＞m2，
为了使两球发生正碰，两小球的半径相同，r1=r2
（3）为了保证入砰小球的速度每一次都相等，小球每次都要从同一个位置滚下；
（4）碰撞前小球的速度最大，所以距离最远的P为碰前入射小球落点的平均位置；碰后的入射小球在被碰小球的后面，所以速度最小，所以最近的M为碰后入射小球的位置，中间的N为碰后被碰小球的位置．
（5）找小球落地点时，一定要重复多次，找出小球落地点的平均位置，其方法是用圆规画一尽可能小的圆，将所有落点圈进，其圆心代表平均落点．
（6）碰撞前入射小球的速度v0=OP

本题解析：

本题难度：一般

4、选择题  两个小球在一条直线上相向运动，若它们相互碰撞后都停下来，则两球碰前 (    )
A．质量一定相等
B．速度大小一定相等
C．总动量一定为零
D．动量一定相同