1、计算题  如图所示，将两条磁性很强且完全相同的磁铁分别固定在质量相等的小车上，水平面光滑，开始时甲车速度大小为3m/s，乙车速度大小为2 m/s，相向运动并在同一条直线上，当乙车的速度为零时，甲车的速度是多少？若两车不相碰，试求出两车距离最短时，乙车速度为多少?

参考答案：解：
（1）对甲乙两车组成的系统，动量守恒取甲的运动方向为正方向
3m－2m＝mv甲＋0，V甲＝；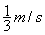
（2）当两车距离最短时，两车具有共同速度
3m－2m＝2mv共，V共＝。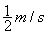

本题解析：

本题难度：一般

2、计算题  一辆小车在光滑的水平面上以v2=1m/s的速度向右运动，小车的质量为M=100kg，如图所示。一质量为m=50kg的人从小车的右端迎面跳上小车，接触小车前瞬间人的水平速度大小为v1=5.6m/s。求人跳上小车后，人和小车共同运动速度的大小和方向。

参考答案：解：取向右为正方向


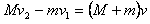
速度大小为1.2m/s，方向向左

本题解析：

本题难度：一般

3、计算题  （19分）一轻质弹簧，两端连接两滑块A和B，已知mA=0．99kg， mB=3kg，放在光滑水平桌面上，开始时弹簧处于原长。现滑块A被水平飞来的质量为mC=10g，速度为400m/s的子弹击中，且没有穿出，如图所示，试求：

（1）子弹击中A的瞬间A和B的速度
（2）以后运动过程中弹簧的最大弹性势能
（3）B可获得的最大动能

参考答案：（1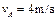），vb=0
（2）6 J
（3）6 J

本题解析：
（1）子弹击中滑块A的过程，子弹与滑块A组成的系统动量守恒
mC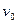=（mC+mA）vA?（2分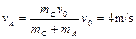）??（2分）?vb="0?" （1分）
（2）对子弹、滑块A、B和弹簧组成的系统，A、B速度相等时弹性势能最大。
根据动量守恒定律和功能关系可得：
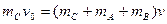?（2分）

m/s

本题难度：一般

4、简答题  如图所示，在光滑水平面上有木块A和B，mA=0.5kg，mB=0.4kg，它们的上表面是粗糙的，今有一小铁块C，mC=0.1kg，以初速v0=10m/s沿两木块表面滑过，最后停留在B上，此时B、C以共同速度v=1.5m/s运动，求：
（1）A运动的速度vA=？
（2）C刚离开A时的速度vC′=？

参考答案：（1）A、B、C三个木块组成的系统动量守恒，以C的初速度方向为正方向，
在整个过程中，由动量守恒得：mCv0=mAvA+（mB+mC）v，
解得：vA=0.5m/s；
（2）A、B、C三个木块组成的系统动量守恒，以C的初速度方向为正方向，
当C刚离开A时AB有共同的速度vA，对A、B、C组成的系统，由动量守恒定律得：
mCv0=（mA+mB）vA+mC vC′，
解得：vC′=5.5m/s；
答：（1）A运动的速度为0.5m/s；
（2）C刚离开A时的速度为5.5m/s．

本题解析：

本题难度：一般

5、填空题  两条船在静止的水面上沿着平行的方向匀速直线滑行，速率都是6.0 m/s，当两船相错时，各给了对方20kg的货物，此后乙船速率减为4.0 m/s、方向不变，若甲船原来的总质量是300kg，则甲船交换货物后的速度为       m/s，乙船原来的总质量为        kg。

参考答案：5.2 ， 120

本题解析：以乙船和甲送出的货物为研究对象，列动量守恒方程
可解得，
以甲船和乙送出的货物为研究对象，列动量守恒方程
（注意）
解得，
考点：考查了动量守恒定律的应用
点评：本题难度偏难，关键是以船和抛出的货物为研究对象

本题难度：一般