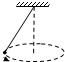
1、简答题  如图所示，在一根不可伸长的细线上系一个质量为m的小球，当把小球拉到使细线与水平面成θ=30°角时，轻轻释放小球．不计空气阻力，求小球落到悬点正下方的B点时对细线的拉力．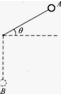

参考答案：

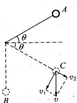
如图所示，当小球下落到C点，细绳偏下与水平成θ角，细绳张紧，小球速度
v=

本题解析：

本题难度：一般

2、简答题  用一条绝缘细线悬挂一个带电小球，小球质量m=2.0×10-2kg，电荷量q=+1.0×10-8C．现加一水平方向的匀强电场，小球平衡于O点时绝缘细线与竖直方向的夹角θ=37°，如图所示．（取g=10m/s2，sin37°=0.6，cos37°=0.8）试求：
（1）该匀强电场的电场强度E的大小；
（2）若将小球沿圆弧OA拉至悬点正下方A点自由释放后，小球作往复运动，则经过O点时细线对小球的拉力．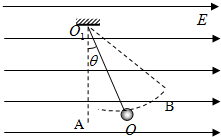

参考答案：（1）小球受力平衡时，受到重力、电场力与绳子的拉力，其中：qE=mgtanθ
所以：E=mgtanθq=1.5×107N/C
（2）A到O的过程中，电场力做正功，重力做负功，设细线的长度为L，则：
qELsinθ-mgL(1-cosθ)=12mv2
在O点：F拉-mgcosθ=mv2L
联立以上2公式，解得：F拉=0.35N
答：匀强电场的电场强度E的大小1.5×107N/C；经过O点时细线对小球的拉力是0.35N．

本题解析：

本题难度：一般

3、简答题  一根长L=80cm的绳子系着一个小球，小球在竖直平面内做圆周运动，已知球的质量为m=0.5kg，g取10m/s2，求：
（1）试确定到达最高点时向心力的最小值
（2）当小球在最高点时的速度为3m/s，绳对小球的拉力
（3）试证明：在能够完成竖直平面内做圆周运动的情况下，无论小球的初速度怎样，在最低点和最高点时绳子上的张力差总为30N．（不计空气阻力）

参考答案：（1）小球在最高点受重力和拉力，合力提供向心力，当拉力为零时，向心力最小，为mg=5N；
（2）当小球在最高点时的速度为3m/s时，拉力和重力的合力提供向心力，有：
F+mg=mv2R
解得：F═mv2R-mg=0.625N；
（3）设最高点速度为v1，最低点速度v2，根据动能定理，有：
mg?2R=12mv22-12mv21；
最高点，有：mg+T1=mv21R；
最低点，有：T2-mg=mv22R；
拉力差为：△T=T1-T2；
联立解得：△T=6mg=30N；
答：（1）到达最高点时向心力的最小值为5N；
（2）当小球在最高点时的速度为3m/s，绳对小球的拉力为0.625N；
（3）证明如上．

本题解析：

本题难度：一般

4、选择题  如图所示，用细线系着一个小球，使小球在水平面内做匀速圆周运动，不计空气阻力，关于小于受力的说法，正确的是（　　）
A．只受重力作用
B．只受拉力作用
C．同时受重力和拉力作用
D．同时受重力、拉力和向心力作用