1、实验题 利用图示装置可以测定喷枪喷射油漆雾滴的速度。
将直径D = 40cm的纸带环,安放在一个可以匀速转动的转台上,纸带上有一狭缝A,A的正对面有一条标志线。油漆喷枪放在开有狭缝B的纸盒里。转台以角速度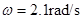 稳定转动后,开始喷漆,喷出来的雾滴运动速度认为不变。仅当狭缝A和B正对平行时,雾滴才能进入纸带环。改变喷射速度
稳定转动后,开始喷漆,喷出来的雾滴运动速度认为不变。仅当狭缝A和B正对平行时,雾滴才能进入纸带环。改变喷射速度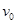 重复实验,已知
重复实验,已知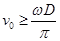 ,在纸带上留下了一系列的痕迹 a、b、c、d。将纸带取下放在刻度尺下,如图所示。
,在纸带上留下了一系列的痕迹 a、b、c、d。将纸带取下放在刻度尺下,如图所示。


(1)速度最小的雾滴所留的痕迹应为?点,该点离标志线的距离为?cm。
(2)该喷枪喷出的雾滴的最大速度为?m/s,若考虑空气阻力的影响,该测量值
?真实值(选填“大于”“小于”或“等于”)。
参考答案:(1) a , 2.50; (2)24,小于;
本题解析:
试题分析:转盘的角速度一定,雾滴速度越大,运行时间越短,在雾滴运行的时间内,转盘转过的角度越小,故雾滴与标志线的距离越近;故a点对应雾滴的速度最小,毫米刻度尺读数要估读,为2.50cm。速度最大的是d点,距离标志线的距离是△s=0.70cm,根据t=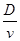 =
=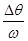 ,Δs=
,Δs= ,解得v=
,解得v=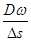 =24m/s;
=24m/s;
若考虑空气阻力,实际上雾滴做减速运动,现在将雾滴当做匀速直线运动的计算,求出来的速度要小于真实的速度。
本题难度:一般
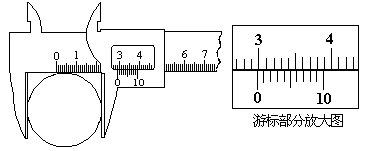
2、实验题 (1)(4分) 一游标卡尺的主尺最小分度为1毫米,游标上有10个小等分间隔,现用此卡尺来测量工件的直径,如图所示。该工件的直径为____________毫米。
(2)(6分)如图A所示的电路中,两二极管均可视为理想二极管,R1=R2。a端对b端的电压与时间的关系如图B的上图所示。请在图B的下图中作出a端对c点的电压与时间的关系图线(最少画一个周期)。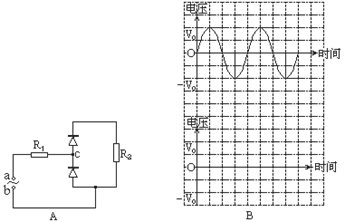
参考答案:
(1)(4分)29.8
(2)(6分)
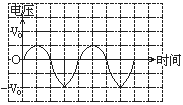
本题解析:(1)游标卡尺的主尺读数为29mm,游标尺读数为8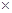 0.1=0.8mm,最后读数为29.8mm。(2)当a端电势高时,只有上方的二极管导通,由图可知,ac间的电压为ab间的电压的一半,当a端电势低时,只有下方的二极管导通,由图可知,ac间的电压与ab间的电压相等,具体图像见答案。
0.1=0.8mm,最后读数为29.8mm。(2)当a端电势高时,只有上方的二极管导通,由图可知,ac间的电压为ab间的电压的一半,当a端电势低时,只有下方的二极管导通,由图可知,ac间的电压与ab间的电压相等,具体图像见答案。
本题难度:简单
3、实验题 “探究加速度与物体质量、物体受力的关系”的实验装置如图1所示。
(1)在平衡小车与桌面之间摩擦力的过程中,打出了一条纸带如图2所示。计时器打点的时间间隔为0.02 s。从比较清晰的点起,每5个点取一个计数点,量出相邻计数点之间的距离。该小车的加速度a=__________m/s2(结果保留两位有效数字)。
(2)平衡摩擦力后,将5个相同的砝码都放在小车上。挂上砝码盘,然后每次从小车上取一个砝码添加到砝码盘中,测量小车的加速度。小车的加速度a与砝码盘中砝码的总重力F的实验数据如下表:
砝码总重力F(N)
| 0.196
| 0.392
| 0.588
| 0.784
| 0.980
|
加速度a(m?s-2)
| 0.69
| 1.18
| 1.66
| 2.18
| 2.70
|
请根据实验数据,在图3中作出a—F图线(画在答题纸上)
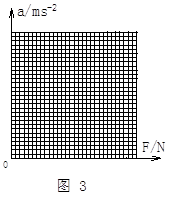
(3)根据提供的实验数据,作出的a—F图线不经过原点,主要原因是________________________ 。
参考答案:0.16?计算F时忘记加入砝码盘的重力,使图象向左平移?
本题解析:(1)根据逐差法并通过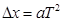 ,即加速度为0.16 m/s2
,即加速度为0.16 m/s2
(2)绘图数据如图
(3)数据表明,当F=0时,就有加速度,说明平衡摩擦过度,或者计算F时忘记加入砝码盘的重力。
点评:本题考查了探究加速度与物体质量、物体受力的关系的研究方法。并考察了这个过程中的摩擦力处理以及数据处理。
本题难度:一般
4、选择题  如图所示,两个质量相同的同种材料物体A、B紧靠在一起放在粗糙的水平面上,如果它们分别受到水平推力F1和F2,且F1>F2,则A、B间的弹力大小为
如图所示,两个质量相同的同种材料物体A、B紧靠在一起放在粗糙的水平面上,如果它们分别受到水平推力F1和F2,且F1>F2,则A、B间的弹力大小为
A.F1
B.F2
C.(F1-F2)/2
D.(F1+F2)/2
参考答案:D
本题解析:分析:先以两个物体整体为研究对象,由牛顿第二定律求出加速度,再隔离其中一个物体研究,求出1施于2的作用力大小.
解答:设两物体的质量均为m,1施于2的作用力大小为F.
根据牛顿第二定律得
? 对整体:a=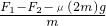
? 对物体2:F-F2-μmg=ma
得到F=ma+F2+μmg= (F1+F2)
(F1+F2)
故选D.
点评:本题是连接体问题,考查灵活选择研究对象的能力,往往用整体法求加速度,而求内力时必须用隔离法.
本题难度:简单
5、简答题 如图所示,一轻质弹簧的一端固定于倾角为θ的光滑斜面上端,另一端系一质量为m的小球,小球被一垂直于斜面的挡板A?挡住,此时弹簧恰好为自然长度.现使挡板A以恒定加速度a(a<gsinθ)匀加速沿斜面向下运动(斜面足够长),已知弹簧的劲度系数为k.
(1)求小球开始运动时挡板A对小球提供的弹力;
(2)求小球从开始运动到与档板分离弹簧的伸长量;
(3)问小球与档板分离后能否回到出发点?请简述理由.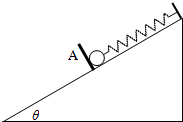
参考答案:(1)设小球受挡板的作用大小为N,刚开始时,弹簧为自然长度,对小球无作用力.
由牛顿第二定律,得
? mgsinθ-N=ma,
得 N=mgsinθ-ma
(2)小球与档板分离时弹力N=0,有 mgsinθ-F=ma,
得 F=mgsinθ-ma
由胡克定律得弹簧的伸长量 △x=Fk=mgsinθ-mak
(3)小球再能回到出发点是不可能的.因为若小球再能回到出发点,则对于整个运动过程来说,由于挡板做负功而机械能减小,这将出现矛盾.
答:( 1 )小球刚开始运动时挡板对小球提供的弹力大小F=mgsinθ-ma.
(2)小球从开始运动到与档板分离弹簧的伸长量为mgsinθ-mak.
(3)小球再能回到出发点是不可能的.因为若小球再能回到出发点,则对于整个运动过程来说,由于挡板做负功而机械能减小,这将出现矛盾.
本题解析:
本题难度:一般