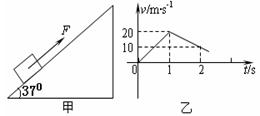
1、计算题  如图甲所示，质量为m＝1kg的物体置于倾角为θ＝37°固定斜面上（斜面足够长），对物体施加平行于斜面向上的恒力F，作用时间t1＝1s时撤去拉力，物体运动的部分v-t图像如图乙所示，设物体受到的最大静摩擦力等于滑动摩擦力，取g=10m/s2。（sin37°=0.6,cos37°=0.8）试求：

（1）物体与斜面间的动摩擦因数；
（2）拉力F的大小；
（3）t=4s时物体的速度.

参考答案：（1）? μ="0.5" （2） F=30N?（3）v=2m/s?方向沿斜面向下（不给方向扣1分）

本题解析：（1）物体在拉力作用下沿斜面向上做匀加速运动，撤去拉力后物体做匀减速运动
物体减速运动时，由v-t图像可得加速度a2=10m/s2
由牛顿第二定律有mgsin37°+μmgcos37°=ma2
解得μ=0.5
（2）物理加速匀速时，由v-t图像可的加速度a1=20m/s2
（3）由牛顿第二定律有F-（mgsin37°+μmgcos37°）=ma2
解得F=30N
（4）由图像得物体在她t=3s时减速为零，由于μ=0.5，即μ<tan37°，物块不能保持静止，要沿斜面向下加速运动，设加速度为a3
由牛顿第二定律有mgsin37°-μmgcos37°=ma3
解得a3=2m/s2
物体向下加速运动时间1s，由v=a3t得v=2m/s

本题难度：一般

2、简答题  传送带在工农业生产中有着广泛的应用．如图所示，平台上的人欲通过一根平行于传送带的轻绳将物品拉上平台，已知物品质量m=50kg，可看成质点，用F=500N的恒力从静止开始往上拉，传送带与水平面的夹角θ=37°，从传送带底端到平台左边的距离L=2.25m，传送带以恒定速度v=2m/s顺时针运行，物品与传送带之间的动摩擦因数μ=0.5，设最大静摩擦力等于滑动摩擦力．（g取10m/s2，sin?37°=0.6，cos?37°=0.8）问：
（1）物品从传送带底端运动到平台上所用的时间是多少？
（2）若在物品离传送带底端L0=0.44m处时，立即撤去恒力F，求物品再经过多少时间离开传送带？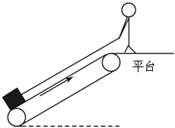

参考答案：（1）物品在达到传送带速度之前，由受力情况，据牛顿定律有：F+μmgcos37°-mgsin37°=ma1
解得：a1=8m/s2
由?v=at?和x=12at2得：
t1=0.25s?x=0.25m?
随后由受力情况，据牛顿定律有：F-μmgcos37°-mgsin37°=ma2
解得：a1=0?即物品随传送带匀速上升
位移：x2=L-x1=2m
T2=x2v=1s
总时间：t=t1+t2=1.25s?
（2）L0=0.44m＞x1=0.25，物品的速度大于传送带的速度v=2m/s
撤去外力F，由物品受力情况，所牛顿定律有：μmgcos37°-mgsin37°=ma3
代入数据解得：a3=-2m/s2
由?2ax=v2t-v20
代入数据解得：X3=1m?
因为L0+x3=1.44m＜L=2.25m?物品速度减为零后倒回传送带底部，
由?x=v0t+12at2
代入数据解得：t3=2.2s?
答：（1）物品从传送带底端运动到平台上所用的时间是1.25s
（2）若在物品离传送带底端L0=0.44m处时，立即撤去恒力F，物品再经过2.2s离开传送带．

本题解析：

本题难度：一般

3、选择题  某人乘电梯从1楼到9楼，经历了加速→匀速→减速的运动过程，则电梯的支持力对人做功情况（　　）
A．加速时做正功，匀速、减速时做负功
B．加速、匀速、减速的过程，都始终做正功
C．加速、匀速时做正功，减速时做负功
D．加速时做正功，匀速时不做功，减速时做负功

参考答案：根据力对物体做功的定义W=FScosθ（其^91考试网式中θ是力F与位移S间的夹角），可知若0°≤θ＜90°，则力F做正功；
若θ=90°，则力F不做功；若90°＜θ≤180°，则力F做负功（或者说物体克服力F做了功）．
人乘电梯从一楼到20楼，在此过程中，他虽然经历了先加速，后匀速，再减速的运动过程，但是支持力的方向始终向上，与位移方向一致，即θ=0°，所以支持力始终做正功．
故选B

本题解析：

本题难度：简单

4、填空题  平地面上运动的小车车厢底部有一质量为m1的木块，木块和车厢通过一根水平轻弹簧相连接，弹簧的劲度系数为k。在车厢的顶部用一根细线悬挂一质量为m2的小球。某段时间内发现细线与竖直方向的夹角为θ，在这段时间内木块与车厢也保持相对静止，如图所示。不计木块与车厢底部的摩擦力，则在这段时间内弹簧的形变量为?。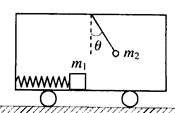

参考答案：

本题解析：m2小球受重力和绳子的拉力，合外力方向水平向左，加速度为，m1的合外力为弹簧的弹力，所以，计算可得弹簧形变量为
故答案为：

本题难度：简单

5、简答题  如图所示，A和B是两个带有同种电荷小球，电量分别为10-3c和10-6c，C是不带电的绝缘木块，B的质量为2Kg，C的质量为3.625Kg，其中A固定在绝缘地面上，B、C恰能悬浮在A的正上方某处，现对C施加一竖直向上的力F，使B、C一起以2.5m/s2加速度竖直向上做匀加速运动．已知静电力常量为k=9×109Nm2/c2，求：
（1）B经过多长时间就要与C脱离．
（2）B在与C脱离前的运动过程中系统电势能减少了4.0625J，求外力F对物体做功为多少？

参考答案：（1）开始时，B、C恰能悬浮在A的正上方某处，
BC整体受重力和A对B的库仑力，由平衡得：
KqCqBr12=(mB+mC)a? ①
当BC间的作用力为零时BC开始分离，此时B受重力和A对B的库仑力，由牛顿第二定律得：
KqCqBr22-mBg=mBa? ②
设B经过时间t就要与C脱离，由x=12at2得：
r2-r1=12at2? ③
①②③联立代入数据求得 t=0.4s
（2）从开始到得B、C将要分离时速度为v，
则 v=at=2.5×0.4m/s=1m/s? ④
设电场力做功为W，外力做功为WF
由功能关系得：W=-△EP=-（-4.0625）J=4.0625J? ⑤
由动能定理得：W+WF-(mB+mC)g(r2-r1)=12(mB+mC)v2? ⑥
④⑤⑥联立代入数据得：WF=10J
答：B经过0.4s就要与C脱离，外力F对物体做功为10J．

本题解析：

本题难度：一般