1、选择题  “嫦娥二号”探月卫星在月球上方100km的圆形轨道上运行．已知“嫦娥二号”卫星的运行周期、月球半径、月球表面重力加速度、万有引力常量G．根据以上信息不能求出（　　）
A．卫星所在处的加速度
B．月球的平均密度
C．卫星线速度大小
D．卫星所需向心力

参考答案：A、根据万有引力等于重力GMmR2=mg，可求出月球的质量M=gR2G，根据GMmr2=mr（2πT）2，求出嫦娥二号的轨道半径r=3gR2T24π2

本题解析：

本题难度：一般

2、选择题  据美国媒体报道，美国和俄罗斯的两颗通信卫星于2009年2月11日在西伯利亚上空相撞，这是人类有史以来的首次卫星在轨碰撞事件．碰撞发生的地点位于西伯利亚上空490英里（约790公里），比国际空间站的轨道高270英里（约434公里）．若两颗卫星的运行轨道均可视为圆轨道，下列说法正确的是（　　）
A．碰撞后的碎片若受到大气层的阻力作用，轨道半径将变小，则有可能与国际空间站相撞
B．在碰撞轨道上运行的卫星，其周期比国际空间站的周期小
C．美国卫星的运行周期大于俄罗斯卫星的运行周期
D．在同步轨道上，若后面的卫星一旦加速，将有可能与前面的卫星相撞

参考答案：A、碰撞后的碎片若受到大气层的阻力作用，轨道半径将变小，则有可能与国际空间站相碰撞．故A正确．
B、根据GMmr2=mr4π2T2得，T=

本题解析：

本题难度：一般

3、选择题  国家卫星海洋应用中心近日透露，2020年前，我国将发射8颗海洋系列卫星，加强对我国黄岩岛、钓鱼岛以及西沙、中沙和南沙群岛全部岛屿附近海域的监测．假设某颗海洋卫星的轨道半径为地球半径的4倍，周期为地球自转周期的

参考答案：对于环绕天体绕中心天体运动，设中心天体的质量为M，环绕天体的质量为m，轨道半径为r，中心天体的半径为R，周期为T，则根据万有引力提供向心力GMmr2=m4π2T2r
解得中心天体的质量为：M=4π2r3GT2
所以中心天体的密度为ρ=MV=4π2r3GT243πR3=3πr3GT2R2
对于某颗海洋卫星绕地球运动，轨道半径为地球半径的4倍，周期为地球自转周期的12，所以ρ地=3π(4R地)3G(12T自)2R地3=3π×43G(12T自)2
对于“嫦娥三号”绕月球的运动，月球的密度为ρ月=3πGT2
因为ρ地=ρ月
所以3π×43G(12T自)2=3πGT2
所以T=T自16=2416h=1.5h．故B正确、ACD错误．
故选：B．

本题解析：

本题难度：简单

4、选择题  某行星的卫星，在靠近行星的轨道上运行，若要计算行星的密度，唯一要测量出的物理量是（万有引力常量已知）（　　）
A．行星的半径
B．卫星的半径
C．卫星运行的线速度
D．卫星运行的周期

参考答案：根据密度公式得：
ρ=MV=M43πR3
A、已知行星的半径，不知道质量，无法求出行星的密度，故A错误．
B、已知卫星的半径，无法求出行星的密度，故B错误．
C、已知飞船的运行速度，根据根据万有引力提供向心力，列出等式可以表示出行星的质量，但是代入密度公式无法求出行星的密度，故C错误．
D、根据根据万有引力提供向心力，列出等式：GMmR2=mR（2πT）2? 得行星的质量：M=4π2R3GT2
代入密度公式得：ρ=3πGT2，
故选D．

本题解析：

本题难度：一般

5、选择题  某人造地球卫星绕地球做匀速圆周运动，实施变轨后卫星的线速度减小到原来的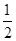，此时卫星仍做匀速圆周运动，则
A．卫星的向心加速度减小到原来的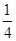
B．卫星的角速度减小到原来的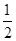
C．卫星的周期增大到原来的8倍
D．卫星的轨道半径增大到原来的4倍

参考答案：CD

本题解析：
试题分析:人造卫星绕地球做匀速圆周运动，它受到地球的万有引力充当向心力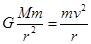，，得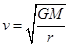，可知，实施变轨后卫星的线速度减小到原来的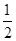，则半径是原来的4倍，故D正确；由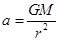，可知卫星的向心加速度减小到原来的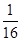，故A正确，由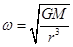，得卫星的角速度减小到原来的，故B错误，由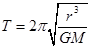可知，卫星的周期增大到原来的8倍，故C正确。

本题难度：一般