1、简答题  

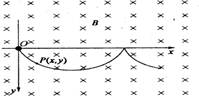
在场强为B的水平匀强磁场中，一质量为m、带正电q的小球在O静止释放，小球的运动曲线如图所示．已知此曲线在最低点的曲率半径为该点到z轴距离的2倍，重力加速度为g．求：
(1)小球运动到任意位置P(x，y)的速率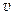
(2)小球在运动过程中第一次下降的最大距离ym.
(3)当在上述磁场中加一竖直向上场强为E()的匀强电场时，小球从O静止释放后获得的最大速率．?

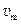参考答案：
（1）?
（2）
（3）

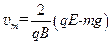
本题解析：

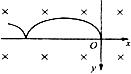
⑴洛伦兹力不做功，由动能定理得 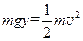?①
解得 ?②
⑵设在最大距离处的速率为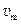，根据圆周运动有
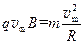?③
且由②知 ?④
由③④及得 ?⑤
⑶小球运动如图所示，由动能定理得 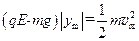?⑥
由圆周运动得 ?⑦
且由⑥⑦及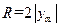解得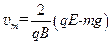

本题难度：一般

2、简答题  如图，足够长的光滑绝缘斜面与水平面的夹角为α=370，其置放在有水平方向的匀强电场和匀强磁场中，电场强度E=50V/m，方向水平向左，磁场方向垂直纸面向外，一个电荷量q=+4.0×10-2C、质量m=0.40kg的光滑小球，以初速度V0=20m/s从底端向上滑动，然后又向下滑动，共经过3s脱离斜面。求该磁场的磁感应强度。（g取10m/s2）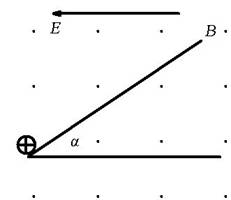

参考答案：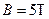

本题解析：分析：小球在上升过程中受到垂直于斜面向下的洛仑兹力，尽管洛仑兹力越来越小，但由于其沿运动方向的分力为零，不影响小球沿斜面做匀减速直线运动，可依据牛顿第二定律和运动学公式求出上升时间t1，在下滑的过程中，洛仑兹力垂直于斜面向上且越来越大，当垂直斜面向上的支持力不断减小直到减为零时，小球脱离斜面，在该方向上建立方程，再结合牛顿第二定律便可求解。
解：小球沿斜面向上运动的过程中受力如图所示。

由牛顿第二定律知：
，
，
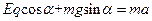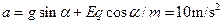则上行时间为: 。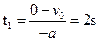
小球在下滑的过程中受力如图，小球在离开斜面之前做匀加速直线运动。

，
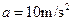运动时间为：t2=t－t1=1s，
脱离斜面时的速度：v=at2=10m/s，
在垂直于斜面方向有：
，
。

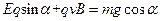本题难度：一般

3、选择题  如图15-5-16所示，带电粒子以水平速度v0垂直进入正交的匀强电场和匀强磁场区域里，穿出磁场区域的速度为v，电场强度为E，磁感应强度为B，则粒子的轨迹、v与v0的大小关系为(? )

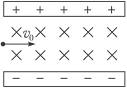
图15-5-16
A．要使粒子能沿直线运动，正电荷应从左边射入，负电荷应从右边射入
B．当v0=E/B时，粒子沿直线运动，且v=v0
C．当v0<E/B时，粒子沿曲线运动，且v>v0
D．当v0>E/B时，粒子将向上偏转

参考答案：BC

本题解析：此题为速度选择器模型.在图示电场和磁场方向下，粒子只有从左侧入射且大小满足v0=E/B时，才能被选择，与电性无关，粒子做匀速直线运动v=v0,选项A错误，B正确.当v0<E/B时，若为正粒子则将向下偏转，电场力做正功，粒子动能增加，v>v0，若为负粒子则将向上偏转，电场力仍做正功，粒子动能也增加，v>v0,故C正确.D中电性不确定，无法判断偏转方向.综上知B、C选项正确.

本题难度：简单

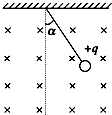
4、选择题  用绝缘细线悬挂一个质量为m，带电荷量为+q的小球，让它处于如图所示的磁感应强度为B的匀强磁场中．由于磁场的运动，小球静止在如图位置，这时悬线与竖直方向夹角为α，并被拉紧，则磁场的运动速度和方向可能是（　　）
A．v=