1、简答题  如图所示，坐标系xOy位于竖直平面内，空间中有沿水平方向、垂直纸而向外的匀强磁场，磁感应强度大小为B，在x＞0的空间内有沿x轴正方向的匀强电场，电场强度大小为E．一带正电荷的小球从图中x轴上的M点沿着与水平方向成θ=30°角的斜向下的直线做匀速运动，进过y轴上的N点进入x＜0的区域．要使小球进入x＜0的区域后能在竖直面内做匀速圆周运动，需要在x＜0的区域内另加一匀强电场．已知带电小球做圆周运动时通过y轴上的P点（P点未标出），重力加速度为g，求：
（1）小球运动的速度大小；
（2）在x＜0的区域内所加匀强电场的电场强度的大小和方向；
（3）N点与P点间的距离．

参考答案：（1）对小球在MN段的运动进行受力分析（如右图所示），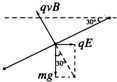
因小球做匀速直线运动，所以有：
qvBsin30°=qE　
解得：小球运动的速度大小为 v=2EB．
（2）在x＜0的区域内，设所加的电场强度为E′，则由运动情况分析知，小球受的重力mg必与电场力qE′是一对平衡力，即有：
qE′=mg　
又 mgtan30°=qE　
故可得：E′=

本题解析：

本题难度：一般

2、计算题  静止的原子核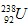处在一个匀强磁场中，当它自发地放出一个α粒子后变成一个新核。若α粒子放出时的速度方向与磁感应强度方向垂直，则
(1)α粒子与新生核做匀速圆周运动的轨道半径之比为多少？
(2)从α粒子放出到它与新生核相遇的过程中，α粒子至少转多少圈？

参考答案：解：(1)粒子在磁场中运动时由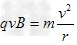
得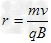，又
而α粒子与新核动量大小相等，
所以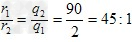
(2)因为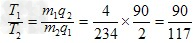
90与117的最小公倍数为1170
所以

本题解析：

本题难度：一般

3、选择题  1998年6月3日，美国发射的航天飞机，其中一个关键部件是由中国科学院设计制造的直径为120mm、高为80 mm、中心磁感应强度为0.134T的永磁体，它的主要使命是要探测宇宙空间中可能存在的反物质，特别是宇宙中反氦原子的原子核，若图中的α磁谱仪中的四条径迹分别为质子、反质子、α粒子、反氦原子核经粒子速度选择器后，再进入匀强磁场形成的径迹，则其中反氦原子核的径迹是?

[? ]
A．1?
B．2?
C．3?
D．4

参考答案：B

本题解析：

本题难度：一般

4、计算题  在图所示的圆形区域内，有垂直于圆平面向里的匀强磁场，磁感强度为B。在圆心位置O点有一个放射源，沿圆面向各个方向释放速率均为v的电子，电子的质量为m电量为e，欲使电子均约束在圆形区域内而不射出，求所加圆形区域磁场的最小面积多大？

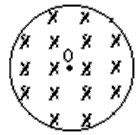
参考答案：解：任取一个电子为研究对象，它从O点射出后将做匀速圆周运动，洛仑兹力提供向心力，即，　　?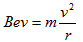
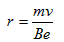粒子在做圆周运动过程中离O点最大距离为2r，所有粒子在运动过程中离O点最大距离均为2r，
所以加一半径2r的圆形磁场即可把电子约束在磁场内，
这个圆形磁场的最小面积： S=π（2r）2 ，

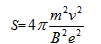
本题解析：

本题难度：一般

5、简答题  磁聚焦被广泛的应用在电真空器件中，如图所示，在坐标xoy中存在有界的匀强聚焦磁场，方向垂直坐标平面向外，磁场边界PQ直线与x轴平行，距x轴的距离为

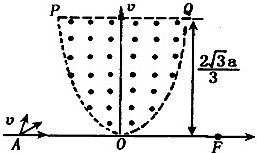
x(a-x) a2 3 -x2 ．且方程对称y轴，在坐标x轴上A处有一粒子源，向着不同方向射出大量质量均为m、电量均为q的带正电粒子，所有粒子的初速度大小相同均为v，粒子通过有界的匀强磁场后都会聚焦在x轴上的F点．已知A点坐标为（-a，0），F点坐标为（a，0）．不计粒子所受重力和相互作用求： （1）匀强磁场的磁感应强度； （2）粒子射入磁场时的速度方向与x轴的夹角为多大时，粒子在磁场中运动时间最长，最长对间为多少？ 参考答案：（1）设磁场的磁感应强度为B，粒子在磁场中做圆周运动的半径为r，圆心为C，从D处射出磁场，其坐标为（x，y），因Rt△CED相似于Rt△DGF 可得yx=a-x 本题解析： 本题难度：一般