1、计算题 (18分)如图,竖直固定轨道abcd段光滑,长为L=1.0m的平台de段粗糙,abc段是以O为圆心的圆弧.小球A和B紧靠一起静止于e处,B的质量是A的4倍.两小球在内力作用下突然分离,A分离后向左始终沿轨道运动, 与de段的动摩擦因数μ=0.2,到b点时轨道对A的支持力等于A的重力的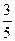 , B分离后平抛落到f点,f到平台边缘的水平距离S= 0.4m,平台高h=0.8m,g取10m/s2,求:
, B分离后平抛落到f点,f到平台边缘的水平距离S= 0.4m,平台高h=0.8m,g取10m/s2,求:
(1)(8分)AB分离时B的速度大小vB;
(2)(5分)A到达d点时的速度大小vd;
(3)(5分)圆弧 abc的半径R.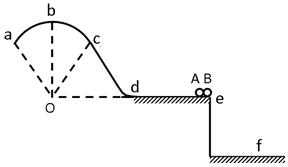
参考答案:(1)vB="1" m/s
(2)vd= 2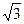 ?m/s
?m/s
(3)R=0.5m
本题解析:
(1)解: (1)B分离后做平抛运动,由平抛运动规律可知:
h=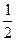 gt2……...3分?vB="s/t" ……...3分)?代入数据得: vB="1" m/s……...2分)
gt2……...3分?vB="s/t" ……...3分)?代入数据得: vB="1" m/s……...2分)
(2)AB分离时,由动量守恒定律得:
mAve=mBvB ……...2分)? A球由 e到d根据动能定理得:
-μmAgl=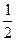 mAvd2-
mAvd2-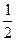 mAve2 ……...2分)?代入数据得: vd= 2
mAve2 ……...2分)?代入数据得: vd= 2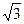 ?m/s……...1分)
?m/s……...1分)
(3)A球由d到b根据机械能守恒定律得:?
mAgR+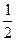 mAvb2=
mAvb2=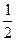 mAvd2……...2分)? A球在b由牛顿第二定律得:
mAvd2……...2分)? A球在b由牛顿第二定律得:
mAg- 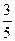 ?mAg=mA vb2/R……...2分)?代入数据得:R=0.5m……...1分)
?mAg=mA vb2/R……...2分)?代入数据得:R=0.5m……...1分)
本题难度:简单
2、实验题 一炮艇总质量为M,以速度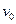 匀速行驶,从船上以相对海岸的水平速度
匀速行驶,从船上以相对海岸的水平速度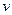 沿前进方向射出一质量为m的炮弹,发射炮弹后艇的速度为
沿前进方向射出一质量为m的炮弹,发射炮弹后艇的速度为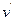 ,若不计水的阻力,则下列各关系式中正确的是?。(填选项前的编号)
,若不计水的阻力,则下列各关系式中正确的是?。(填选项前的编号)
 ①
①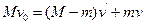 ? ? ②
? ? ② 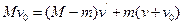
③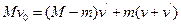 ? ④
? ④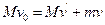
参考答案: ①
①
本题解析:动量守恒定律必须相对于同量参考系。本题中的各个速度都是相对于地面的,不需要转换。发射炮弹前系统的总动量为Mv0;发射炮弹后,炮弹的动量为mv0,船的动量为(M-m)v′所以动量守恒定律的表达式为
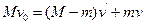
正确选项为①
本题难度:一般
3、选择题 (6分)如图所示,光滑水平面上滑块A、C质量均为m=1kg,B质量为M=3kg.开始时A、B静止,现将C以初速度v0=2m/s的速度滑向A,与A碰后C的速度变为零,而后A向右运动与B发生碰撞并粘在一起,;求:

①A与B碰撞后的共同速度大小;
②A与B碰撞过程中,A与B增加的内能为多少?
参考答案:(1)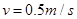 ;(2)1.5J;
;(2)1.5J;
本题解析:①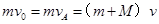 (2分)
(2分)
解得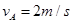 (1分)
(1分)
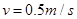 (1分)
(1分)
②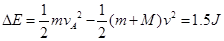 (2分)
(2分)
本题难度:简单
4、填空题 场强为E、方向竖直向上的匀强电场中有两小球A、B,它们的质量分别为m1、m2,电量分别为q1、q2,A、B两球由静止释放,重力加速度为g,则小球A和B组成的系统动量守恒应满足的关系式为_______________。
参考答案:E(q1+q2)=(m1+m2)g
本题解析:
本题难度:一般
5、选择题 质量相等的A、B两球之间压缩一根轻弹簧,静置于光滑水平桌面上,当用板挡住小球A而只释放B球时,B球被弹出落于距桌边为s的水平地面上,如图3所示.问当用同样的程度压缩弹簧,取走A左边的挡板,将A、B同时释放,B球的落地点距桌边为( )

图3
A.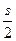 B.
B.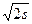 C.s D.
C.s D.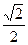 s
s
参考答案:D
本题解析:用当板挡住小球A时,设球在空中飞行时间为t,则由平抛运动知B球的弹出速度vB=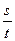 ,弹簧被压缩时具有的弹性势能Ep=
,弹簧被压缩时具有的弹性势能Ep=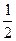 mvB2=
mvB2=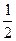 m
m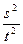 .取去挡板时,由动量守恒得,mvA′=mvB′,由能量守恒得,
.取去挡板时,由动量守恒得,mvA′=mvB′,由能量守恒得,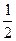 mvA′2+
mvA′2+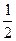 mvB′2=Ep.解得vA′=vB′=
mvB′2=Ep.解得vA′=vB′=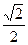 vB,由平抛运动水平分运动得,s′=vB′t=
vB,由平抛运动水平分运动得,s′=vB′t=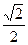 s,故选项D正确,ABC错误.
s,故选项D正确,ABC错误.
本题难度:一般