1、填空题  一探空火箭未打中目标而进入绕太阳的近似圆形轨道运行，轨道半径是地球绕太阳公转半径的９倍，则探空火箭绕太阳公转周期为_______年。

参考答案：27年

本题解析：因为探空火箭和地球都是绕着太阳运动，所以根据开普勒第三定律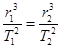可得探空火箭绕太阳公转周期为27年。

本题难度：简单

2、选择题  已知地球半径为R，地球表面的重力加速度为g，若高空中某处的重力加速度为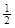g，则该处距地球表面的高度为（?）
A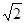．（—1）R
B．R
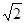C．R
D．2 R

参考答案：A

本题解析：设地球的质量为M，某个物体的质量为m，则在地球表面有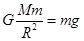：?①
在离地面h高处轨道上有：?②
由?①②联立得：，故选A．
点评：在地球表面，重力提供向心力，在任意轨道，万有引力提供向心力，联立方程即可求解．

本题难度：简单

3、填空题  如图9所示，在发射地球同步卫星的过程中，卫星首先进入椭圆轨道Ⅰ，然后在Q点通过改变卫星速度，让卫星进入地球同步轨道Ⅱ。则该卫星的发射速度?11.2km/s（填大于、小于或等于），卫星在同步轨道Ⅱ上的运行速度必定?7.9km/s （填大于、小于或等于）。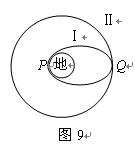

参考答案：小于；小于

本题解析：略

本题难度：简单

4、选择题  甲、乙两个质点间的万有引力大小为F，若甲、乙物体的质量均增加到原来的2 倍，同时它们之间的距离亦增加到原来的2 倍，则甲、乙两物体间的万有引力大小将为（ ）
A．8F
B．4F
C．F
D．2F

参考答案：C

本题解析：两个质点相距r时，它们之间的万有引力为F=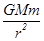，若它们间的距离为2r，各自质量变为原来的2倍，则它们之间的万有引力为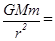F′=F。

本题难度：一般

5、计算题  (15分)一颗人造卫星靠近某行星表面做匀速圆周运动，经过时间t，卫星运行的路程为s，运动半径转过的角度为1 rad，引力常量设为G，求：
(1)卫星运行的周期；
(2)该行星的质量．

参考答案：(1)2πt　(2)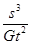

本题解析：(1)卫星的角速度ω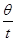＝＝rad/s，
周期T＝＝2πt.
(2)设行星的质量为M，半径为R，则有R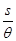＝＝s，由牛顿第二定律得：＝mω2R，解得：M＝.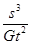

本题难度：一般