1、计算题  在航天事业中要用角速度计可测得航天器自转的角速度ω，其结构如图9所示，当系统绕OO′转动时，元件A在光滑杆上发生滑动，并输出电信号成为航天器的制导信号源。已知A质量为m，弹簧的劲度系数为k，原长为L0，电源电动势为E，内阻不计，滑动变阻器总长为L，电阻分布均匀，系统静止时滑动变阻器触头P在中点，与固定接头Q正对，当系统以角速度ω转动时，求：

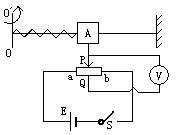
（1）弹簧形变量x与ω的关系式；
（2）电压表的示数U与角速度ω的关系式

参考答案：(1)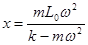?(2)

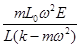
本题解析：（1）由圆周运动规律可得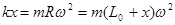，?（3分）
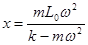得?（3分）
（2）由串联电路的规律得：?（6分）
点评：本题是力与电综合题，关键要寻找力电联系的桥梁．本题力电联系的纽带是弹簧伸长的长度．中等难度．

本题难度：一般

2、简答题  如图所示，质量均为m、电荷量均为q的带负电的一簇粒子从P1（-a，0）点以相同的速率vo在xOy平面内朝x轴上方的各个方向射出（即0＜θ≤π），不计重力及粒子间的相互作用，且已知a足够大．
（1）试在图中的适当位置和区域加一垂直于xOy平面、磁感应强度为B的匀强磁场，使这簇带电粒子通过该磁场后都沿平行于x轴方向运动．在图中定性画出所加的最小磁场区域边界的形状和位置．
（2）试在图中的某些区域再加垂直于xOy平面、磁感应强度为B的匀强磁场，使从Pl点发出的这簇带电粒子通过磁场后都能通过P2（a，0）点．
要求：①说明所加磁场的方向，并在图中定性画出所加的最小磁场区域边界的形状和位置；
②定性画出沿图示vo方向射出的带电粒子运动的轨迹；
③写出所加磁场区域与xOy平面所成截面边界的轨迹方程．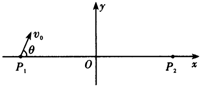

参考答案：

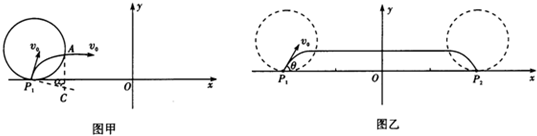
（1）设带电粒子从A点离开磁场区域，A点坐标为（x、y），粒子旋转的半径为R，旋转的圆心在C点，旋转圆心角为α，则
? x=一a+Rsinα，
? y=R-Rcosα，
解得（x+a）2+（y-R）2=R2．
可见，所加磁场的边界的轨迹是一个以（-a，R）为圆心，
半径为R=mv0qB的圆．该圆位于x轴上方且与P1点相切．
（2）根据对称性可得出在P2处所加的磁场最小区域也是圆，同理可求得其方程为（x-a）2+（y-R）2=R2?
圆心为（a，R），半径为R=mv0qB，
由数学知识可知该圆位于x轴上方且与P2点相切；
根据左手定则判断得知，磁场方向垂直于xOy平面向里；
沿图示v0方向射出的带电粒子运动的轨迹如图所示．
答：
（1）所加磁场的边界的轨迹是一个以（-a，R）为圆心，半径为R=mv0qB的圆．该圆位于x轴上方且与P1点相切．
（2）①所加磁场的方向垂直于xOy平面向里；在图中定性画出所加的最小磁场区域边界的形状是圆，该圆位于x轴上方且与P2点相切．如上图所示；
②定性画出沿图示vo方向射出的带电粒子运动的轨迹如图；
③所加磁场区域与xOy平面所成截面边界的轨迹方程为（x-a）2+（y-R）2=R2．圆心为（a，R），半径为R=mv0qB．

本题解析：

本题难度：一般

3、选择题  当汽车通过拱桥顶点的速度为3m/s时，车对桥顶的压力为车重

参考答案：在桥顶，对汽车运用牛顿第二定律有：mg-N=mv2R，N=14mg．解得，R=1.2m．
不受摩擦力作用，则支持力为零，则有mg=mv′2R，解得，v′=

本题解析：

本题难度：简单

4、选择题  如图所示，三段细线长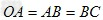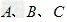，三球质量相等， 当它们绕O点在光滑的水平桌面上以相同的角速度作匀速圆周运动时，则三段线的拉力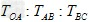为

[? ]
A．?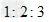
B．?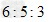
C．?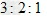
D．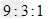

参考答案：B

本题解析：

本题难度：简单

5、计算题  细绳一端系着质量M=8kg的物体，静止在水平面，另一端通过光滑小孔吊着质量m=2kg的物体，M的中点与圆孔的距离r=0.2m，已知M与水平面间的动摩擦因数为0.2，现使此物体M随转台绕中心轴转动，问转台角速度ω在什么范围m会处于静止状态？（g="10" m/s2）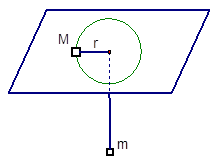

参考答案：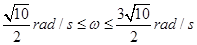

本题解析：当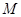所受的摩擦力与拉力反向时，角速度最小.则有：
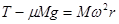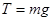??得：
当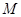所受的摩擦力与拉力同向时，角速度最大.
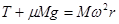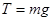??得：?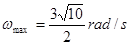
所以：m处于静止状态时转台角速度ω的范围为：?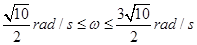
点评：该类型题目关键点在找到两个物体直接的联系，本题中两物体靠轻绳连接，绳子上的力相等是关键，其次静摩擦力方向不确定也是需要注意的地方。

本题难度：一般